Un aspecto usual en la Gestión de Proyectos es enfrentar incentivos económicos por entregas anticipadas o a tiempo en base a la planificación preliminar y adicionalmente multas o cargos por entregas atrasadas o tardías. En este contexto el método PERT (Program Evaluation and Review Technique) permite incorporar de forma explícita la incertidumbre asociada a los tiempos requeridos para completar cada una de las actividades de un proyecto.
Beneficios Esperados de un Proyecto utilizando PERT
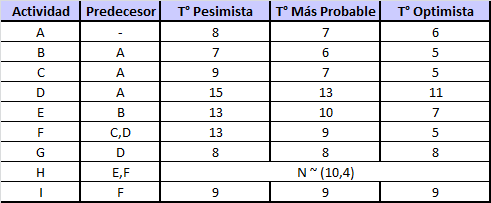
En el siguiente ejemplo se presenta la situación de un proyecto que consta de 9 actividades, cuyas relaciones de precedencia y tiempos en días (pesimista, más probable y optimista) se resumen a continuación:
Donde 
y los tiempos están en días.
Se desea completar el proyecto al cabo de 40 días a contar del inicio de las actividades. En caso de terminar antes de dicho plazo se estima que se accederá a un incentivo monetario de $200.000, no obstante, en caso contrario se asumirá una pérdida de $15.000 por cada día de atraso con un tope máximo de $30.000 (sobre los beneficios estimados). ¿Cuál es la ruta crítica del proyecto?, ¿Cuáles son los beneficios esperados del proyecto?.
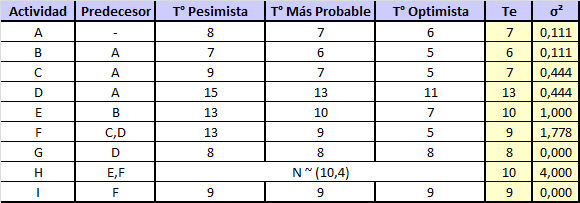
Sabemos que el tiempo esperado para cada actividad se obtiene de 
, por ejemplo, 
. Adicionalmente la varianza se obtiene de 
, por ejemplo, 
. Con la ayuda de Excel resulta sencillo replicar el procedimiento para el resto de las actividades como se muestra a continuación:
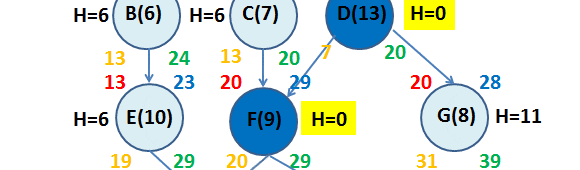
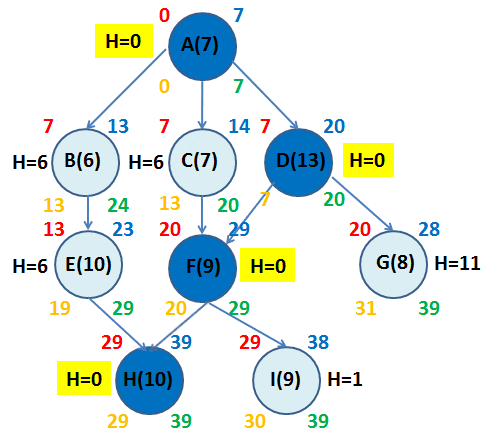
Considerando el Tiempo Esperado (Te) para cada una de las actividades generamos un diagrama de proyecto que nos permita identificar la Ruta Crítica y las holguras (en días) para cada una de las actividades. De esta forma se obtiene que A-D-F-H es la ruta crítica del proyecto con un tiempo esperado para completar éste de 39 días.
Donde los valores con color rojo en la esquina superior izquierda de cada nodo representan el inicio más cercano; los valores con color azul de la esquina superior derecha el término más cercano; los valores de la esquina inferior izquierda con color naranjo el inicio más lejano y finalmente los números con color verde en la esquina inferior derecha representan el término más lejano.
A continuación se requiere estimar la probabilidad de completar el proyecto antes de 40 días, caso en el cual se accede a un beneficio de $200.000.
![\mathbb{P}[T<40]=\mathbb{P}[Z_{\alpha }<\frac{40-39}{\sum {\sigma _{RC}}^{2}}]=\frac{40-39}{\sqrt{(\frac{1}{9})+(\frac{4}{9})+(\frac{16}{9})+4}}\cong0,6544](http://s0.wp.com/latex.php?latex=%5Cmathbb%7BP%7D%5BT%3C40%5D%3D%5Cmathbb%7BP%7D%5BZ_%7B%5Calpha+%7D%3C%5Cfrac%7B40-39%7D%7B%5Csum+%7B%5Csigma+_%7BRC%7D%7D%5E%7B2%7D%7D%5D%3D%5Cfrac%7B40-39%7D%7B%5Csqrt%7B%28%5Cfrac%7B1%7D%7B9%7D%29%2B%28%5Cfrac%7B4%7D%7B9%7D%29%2B%28%5Cfrac%7B16%7D%7B9%7D%29%2B4%7D%7D%5Ccong0%2C6544&bg=ffffff&fg=000000&s=0 "\mathbb{P}[T<40]=\mathbb{P}[Z_{\alpha }<\frac{40-39}{\sum {\sigma _{RC}}^{2}}]=\frac{40-39}{\sqrt{(\frac{1}{9})+(\frac{4}{9})+(\frac{16}{9})+4}}\cong0,6544")
El beneficio esperado en este escenario sería $200.000*0,6544=$130.880.
Por otra parte la probabilidad de que el proyecto demore más de 41 días se obtiene de la siguiente forma:
![\mathbb{P}[T>41]=\mathbb{P}[1-Z_{\alpha }<\frac{41-39}{\sum {\sigma _{RC}}^{2}}]=\frac{41-39}{\sqrt{(\frac{1}{9})+(\frac{4}{9})+(\frac{16}{9})+4}}\cong0,2134](http://s0.wp.com/latex.php?latex=%5Cmathbb%7BP%7D%5BT%3E41%5D%3D%5Cmathbb%7BP%7D%5B1-Z_%7B%5Calpha+%7D%3C%5Cfrac%7B41-39%7D%7B%5Csum+%7B%5Csigma+_%7BRC%7D%7D%5E%7B2%7D%7D%5D%3D%5Cfrac%7B41-39%7D%7B%5Csqrt%7B%28%5Cfrac%7B1%7D%7B9%7D%29%2B%28%5Cfrac%7B4%7D%7B9%7D%29%2B%28%5Cfrac%7B16%7D%7B9%7D%29%2B4%7D%7D%5Ccong0%2C2134&bg=ffffff&fg=000000&s=0 "\mathbb{P}[T>41]=\mathbb{P}[1-Z_{\alpha }<\frac{41-39}{\sum {\sigma _{RC}}^{2}}]=\frac{41-39}{\sqrt{(\frac{1}{9})+(\frac{4}{9})+(\frac{16}{9})+4}}\cong0,2134")
Con un beneficio esperado de $170.000*0,2134=$36.278.
Finalmente evaluamos el caso donde el tiempo del proyecto se encuentra en el intervalo entre 40 y 41 días.
![\mathbb{P}[T\geq40]+\mathbb{P}[T\leq 41]=0,1322](http://s0.wp.com/latex.php?latex=%5Cmathbb%7BP%7D%5BT%5Cgeq40%5D%2B%5Cmathbb%7BP%7D%5BT%5Cleq+41%5D%3D0%2C1322&bg=ffffff&fg=000000&s=0 "\mathbb{P}[T\geq40]+\mathbb{P}[T\leq 41]=0,1322")
Siendo el beneficio esperado de este escenario $185.000*0,1322=$24.457.
En consecuencia el beneficio esperado asociado a completar el proyecto es de $191.615 ($130.880+$36.278+$24.457).