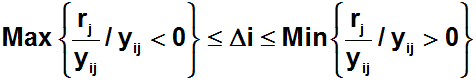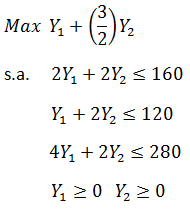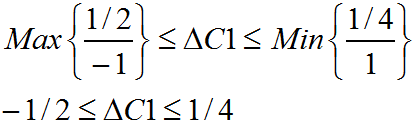En el contexto del Análisis de Sensibilidad o Postoptimal en Programación Lineal y una vez alcanzada la tabla (tableau) final en la aplicación del método simplex, resulta de interés evaluar el impacto en la solución óptima del problema si cambia un coeficiente o parámetro en la función objetivo asociado a una variable básica. Se busca dar respuesta a este escenario sin la necesidad de reoptimizar, es decir, de resolver el problema original nuevamente.
Para conservar la solución óptima identificada inicialmente, se debe cumplir que el costo reducido de todas las variables debe ser mayor o igual a cero (recordar que el costo reducido de las variables básicas es cero por tanto dicha condición en la práctica se establece sobre las variables no básicas). Lo anterior se garantiza si el incremento es cualquiera en el siguiente intervalo:
Donde rj es el costo reducido de la respectiva variable no básica en la actual solución óptima y los coeficientes yij denotan las entradas en la tabla final del método simplex asociadas a la variable básica xi (cuyo costo cambia) y la respectiva variable no básica xj.
Para presentar el concepto anteriormente expuesto consideremos el siguiente problema de Programación Lineal:
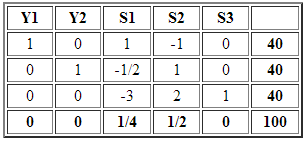
Luego de llevar a la forma estándar, incorporando S1, S2 y S3 como las variables de holgura de las restricciones 1, 2 y 3 respectivamente y resolver el modelo lineal anterior a través del método simplex se alcanza la siguiente tabla óptima:
La solución básica factible óptima es Y1=40 e Y2=40 con valor óptimo V(P)=100. A continuación determinaremos un intervalo de variación para los coeficientes que ponderan a las variables Y1 e Y2 en la función objetivo de modo que conservar la actual solución óptima. En este sentido tanto Y1 como Y2 son variables básicas en el óptimo según se aprecia en la tabla anterior.
Luego el intervalo de variación para C1 (en adelante coeficiente asociado a la variable Y1 en la función objetivo de minimización) que mantiene la solución óptima original es:
Del cálculo anterior se obtiene que C1 (coeficiente que multiplica a la variable Y1 en la función objetivo de minimización) puede variar en el intervalo entre C1℮[-1-1/2, -1+1/4], es decir, C1℮[-3/2, -3/4] y se conserva la actual solución óptima. Si hacemos la equivalencia en la función objetivo de maximización original el intervalo corresponde a C1℮[3/4, 3/2], es decir, existe una reducción permisible de 1/4 y un aumento permisible de 1/2 para el valor actual del parámetro que mantiene la solución óptima inicial. De forma análoga se puede verificar que el intervalo de variación para C2 (en la función objetivo de maximización) corresponde a C2℮[1, 2], con un aumento y disminución permisible de 1/2 en cada caso.
Los resultados obtenidos son consistentes con los que provee el informe de confidencialidad o sensibilidad de Solver según se resume a continuación:
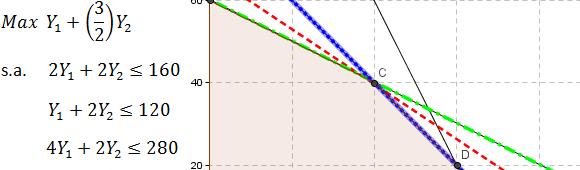
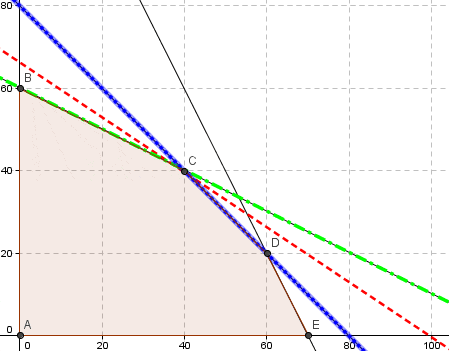
Una alternativa para corroborar los resultados anteriores de una forma intuitiva consiste en realizar una representación gráfica del problema anterior. La solución óptima se encuentra en el vértice C, donde la línea punteada de color rojo representa la curva de nivel que intersecta dicha solución. Por otra parte la línea punteada de color verde se obtiene al modificar C1 a 3/4 (reducción permisible de 1/4), lo cual conserva la solución óptima actual pero deja de ser única (en efecto se genera el caso de infinitas soluciones óptimas en el tramo entre los vértices B y C). Finalmente la línea color azul representa la curva de nivel que resulta de cambiar el coeficiente de C1 a 3/2 (aumento permisible de 1/2) que también conserva la solución actual y denota el caso de infinitas soluciones en el tramo CD).