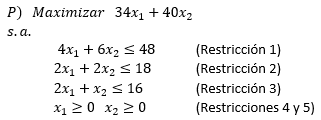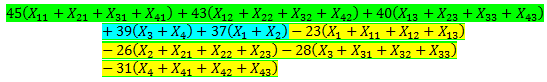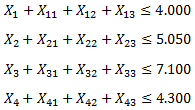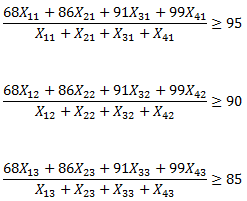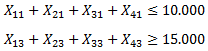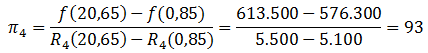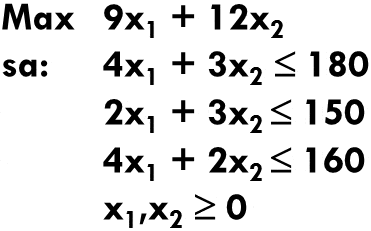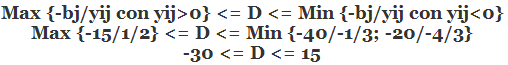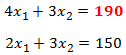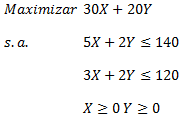precio sombra Archivos - Gestión de Operaciones

Informes de Sensibilidad en Premium Solver Pro (Interpretación)

Las ventajas que ofrece la utilización de una herramienta de optimización profesional como Premium Solver Pro son múltiples y son rápidamente identificadas por quienes comienzan a formarse en el apasionante mundo de la Investigación de Operaciones. Respecto a este tema en particular he tenido el honor de publicar un artículo (en inglés) en el Blog del prestigioso sitio de FrontlineSolvers (desarrolladores del complemento Solver para Excel) llamado How to Correctly Interpret Sensitivity Reports in Premium Solver. En este contexto a continuación presentamos la traducción del mismo a español teniendo en cuenta que parte mayoritaria de nuestros lectores son de países de habla hispana.

En mi experiencia como profesor de Investigación de Operaciones he constatado de forma directa los beneficios de implementar computacionalmente modelos de optimización de distinta complejidad en un ambiente de aprendizaje intuitivo y al mismo tiempo confiable. En este sentido los alumnos adquieren rápidamente las destrezas suficientes para resolver problemas de optimización de distinto tamaño en una plataforma conocida como resulta ser Excel.

Cabe destacar adicionalmente que Premium Solver Pro no solo nos permite resolver modelos de optimización, también ofrece la oportunidad de generar Informes de Sensibilidad una vez alcanzada la solución óptima y valor óptimo de un modelo base. En este contexto el análisis de sensibilidad o postoptimal buscar analizar el impacto que tiene en los resultados de un modelo la modificación de uno o varios parámetros del mismo.

Un Informe de Sensibilidad de Premium Solver Pro se divide en 3 partes:

Función objetivo
Celdas variables
Restricciones

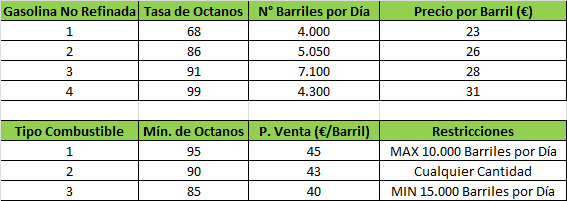
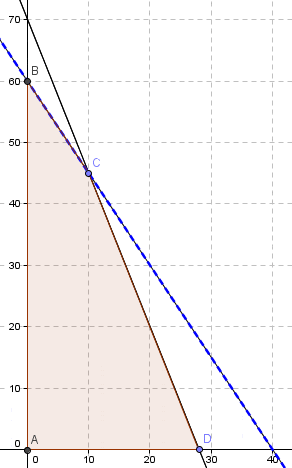
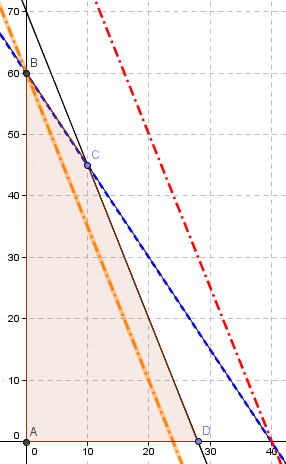
A continuación presentamos un sencillo modelo de Programación Lineal el cual será implementado computacionalmente, obteniendo el Informe de Sensibilidad que analizaremos en detalle con el objetivo de interpretarlo de forma correcta.

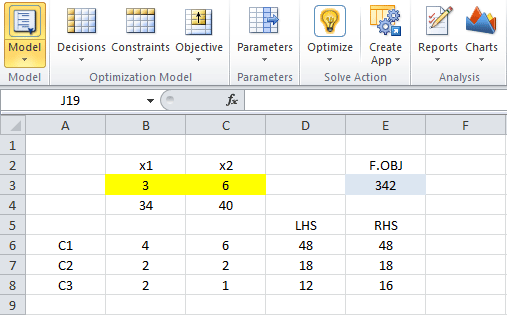
Luego de utilizar Premium Solver Pro para resolver el modelo anterior se alcanza la solución óptima $x_{1}=3$ y $x_{2}=6$ , con valor óptimo $V(PL)=342$ .

A continuación podemos obtener el Informe de Sensibilidad accediendo al módulo Reports > Optimization > Sensitivity, tal cual se muestra a continuación:

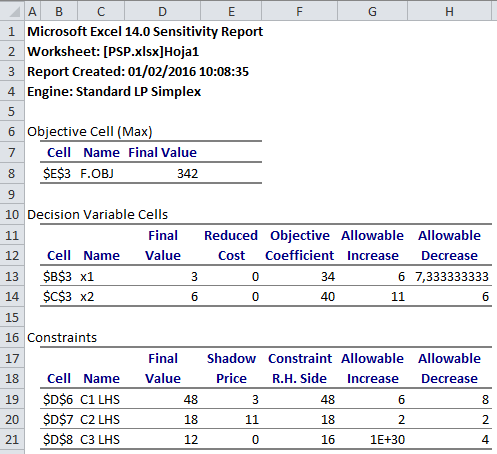
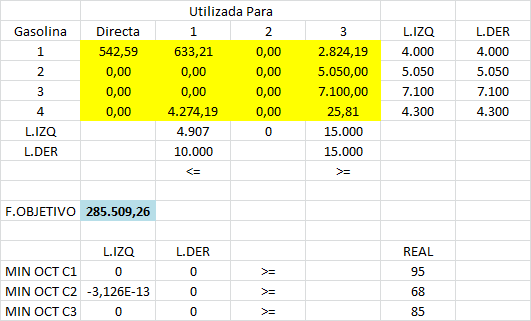
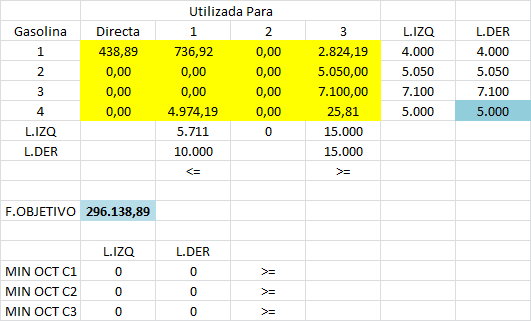
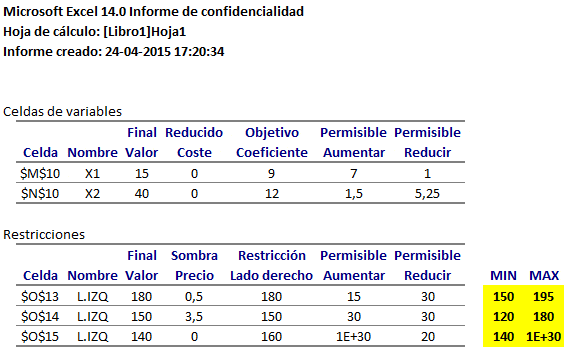
Una vez que solicitemos el Informe de Sensibilidad se generará una nueva hoja en el archivo Excel que estemos trabajando con el reporte de los resultados. Para el ejemplo propuesto en este artículo los resultados son los siguientes:

A continuación detallaremos cómo interpretar cada una de las 3 partes que nos ofrece el Informe de Sensibilidad de Solver.

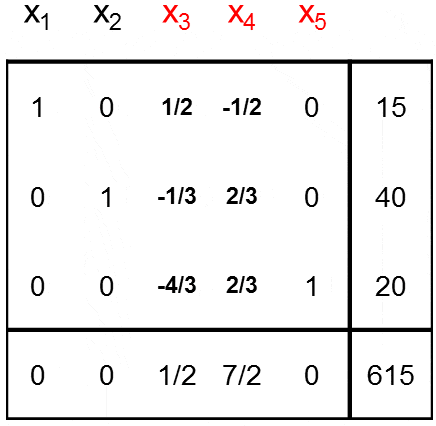
Objective Cell (Max): Se observa que el valor óptimo, es decir, el valor de la función objetivo del problema de maximización al ser evaluada en la solución óptima alcanzada es de 342. Dicho valor se obtiene de: $V(PL)=(34)*3+(40)*6=342$ .

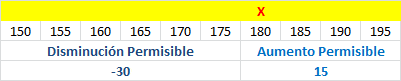
Decision Variable Cells: En esta sección se puede identificar la solución óptima (valores bajo la columna etiquetada como Final Value), los coeficientes o parámetros en la función objetivo (valores en la columna Objective Coefficient), el aumento permisible y la disminución permisible para cada uno de los coeficientes de forma individual en la función objetivo que permite garantizar que se conserva la actual solución óptima.

Por ejemplo, consideremos el coeficiente $c_{1}=34$ asociado a la variable de decisión $x_{1}$ en la función objetivo de maximización. La disminución permisible para dicho parámetro es de 7,333 aprox (equivalente a 22/3) unidades y el aumento permisible de 6, de modo que si $c_{1}\epsilon [34-\frac{22}{3},34+6]$ ==> $c_{1}\epsilon [26,\bar{6},40]$ se conserva la solución óptima original (notar que se asume para este análisis que el resto de los parámetros del modelo mantienen sus valores iniciales). De forma análoga recomendamos al lector verificar que el intervalo de variación para $c_{2}$ que conserva la actual solución óptima es $c_{2}\epsilon [34,51]$ .

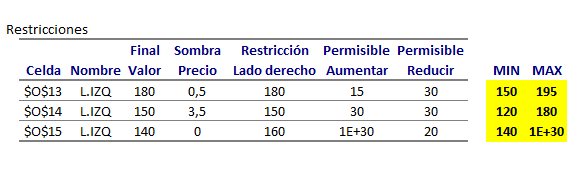
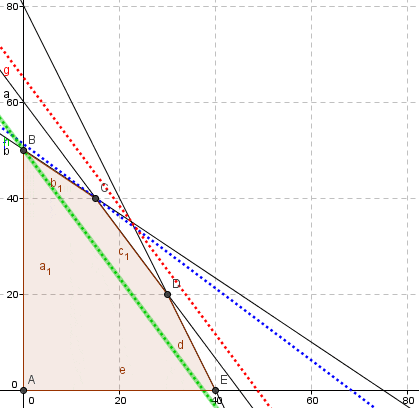
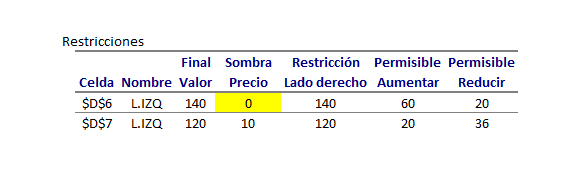
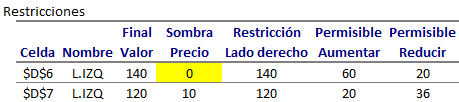
Constraints: Un primer aspecto a observar es si una restricción se encuentra activa al ser evaluada en la solución óptima. Una restricción activa es aquella que se satisface en igualdad. Por ejemplo, se puede ver que para las Restricciones 1 y 2 el valor bajo la columna Final Value es idéntico al lado derecho de la restricción o Constraint R.H. Side. Dicho de otra forma, dado que las Restricciones 1 y 2 son activas en el óptimo, la solución óptima del problema propuesto se puede obtener mediante la resolución de un sistema de ecuaciones con 1 y 2 activas. Notar que adicionalmente la Restricción 3 si bien se satisface no se cumple en igualdad.

También resulta de interés interpretar lo que se conoce como Precio Sombra de una restricción.

El Precio Sombra corresponde a la tasa de cambio del valor óptimo de un modelo de Programación Lineal ante la modificación marginal del lado derecho de una restricción. Se entiende por una modificación marginal aquella que permite conservar la base óptima del problema (idénticas variables básicas originales en el caso del Método Simplex) o la geometría del problema (mantener las restricciones activas originales).

Dada la definición anterior es natural comprender que el Precio Sombra de la Restricción 3 sea cero. Si el lado derecho representa la disponibilidad de un recursos (por ejemplo, horas hombre, unidades de materia prima, etc), en la solución óptima original se utiliza 12 de las 16 unidades disponibles (que es consistente con una disminución permisible de 4 unidades y un aumento permisible de 1E+30 o infinito) para el recurso. Adicionalmente como la Restricción 3 no es activa, cualquier variación del lado derecho de dicha restricción en el intervalo $b_{3}\epsilon [12,+\infty[$ no solo conserva el valor óptimo, sino también la solución óptima original.

El caso de las Restricciones 1 y 2 es diferente. Por ejemplo, si aumenta en una unidad el lado derecho de la Restricción 1, pasando de 48 a 49 unidades (notar que el aumento permisible para dicho parámetro es de 6 unidades) el valor óptimo aumentará de forma proporcional al Precio Sombra de dicha restricción: $V(\bar{P})=V(P)+\Delta b_{1}*\pi _{1}=342+(49-48)*3=345$ . De forma análoga si, por ejemplo, en vez de aumentar el lado derecho de la Restricción 1, disminuye de 48 a 45 (disminución de 3 unidades que está dentro del rango permitido), el nuevo valor óptimo será: $V(\bar{P})=V(P)+\Delta b_{1}*\pi _{1}=342+(45-48)*3=333$ . Recomendamos al lector verificar directamente estos resultados luego de reoptimizar ante los cambios propuestos.

En síntesis queda en evidencia que la utilidad de Premium Solver Pro va más allá de implementar y resolver computacionalmente un modelo de optimización. En este sentido interpretar de forma correcta el análisis de sensibilidad que nos ofrece genera un ahorro de tiempo frente al escenario de reoptimizar que muchas veces es evitable, además de que nos permitir comprender de mejor forma la estructura de una solución óptima, que no sólo se limita a identificar cuál es el valor que alcanzan las variables de decisión en la resolución computacional.

Optimización de la Mezcla de Combustibles en una Refinería

El siguiente problema representa la optimización de la mezcla de combustibles en una refinería con el propósito de maximizar los beneficios asociados a su explotación. En este contexto este caso constituye una variante o extensión del Ejemplo de un Problema de Mezcla de Productos en Programación Lineal y otros conceptualmente similares como el Problema de Producción de Mezcla de Café, entre otros. A continuación los antecedentes de nuestro caso de estudio:

Problema de Mezcla de Combustibles

Una refinería compra 4 tipos de gasolinas no refinadas con las cuales puede fabricar hasta 3 tipos de combustibles para venta al público. La información se resume en la siguiente tabla:

Por ejemplo, la Gasolina No Refinada Tipo 1 tiene 68 Octanos y se dispone de un máximo de 4.000 barriles diarios, donde cada uno de estos barriles se compra a 23 Euros. Así mismo, por ejemplo, el Combustible 1 requiere un mínimo de 95 Octanos y su precio de venta es de 45 Euros el barril. Para el Combustible 1 en particular se establece un máximo de producción de 10.000 barriles diarios.

La refinería puede vender adicionalmente la gasolina no refinada a un precio de 39 Euros el barril si ésta tiene un octanaje mayor o igual a 90 Octanos. Alternativamente el precio de venta se reduce a 37 Euros el barril si el octanaje es inferior a 90 Octanos.

Formule un modelo matemático de Programación Lineal para ayudar a la refinería a maximizar sus ganancias diarias.

Variables de Decisión: Cada tipo de gasolina sin refinar tiene 4 usos posibles: ser vendida directamente o ser utilizada como insumo para producir Combustible tipo 1, 2 y 3.

Función Objetivo: Se desea maximizar la ganancia asociada al proceso de mezcla y venta de combustibles. Con verde se destaca los ingresos asociados a la venta de los 3 tipos de combustibles, con celeste los ingresos que provienen de la venta de gasolinas sin refinar y con color amarillo se descuentan los costos asociados a la compra de las gasolinas sin refinar.

Restricciones:

Disponibilidad de barriles diarios: Cada gasolina no refinada tiene 4 usos posibles: venta directa o como mezcla para elaborar combustible 1, 2 o 3. En cualquier caso su uso no podrá superar el máximo de barriles disponibles.

Octanaje mínimo: El octanaje de la mezcla de cada uno de los 3 combustibles (obtenido como un promedio ponderado de los octanajes de las respectivas gasolinas) debe al menos igualar el requerimiento mínimo establecido en este aspecto.

Límites de venta: No se puede vender más de 10.000 barriles diarios de Combustible 1 y adicionalmente no se puede vender menos de 15.000 barriles diarios de Combustible 3.

No negatividad: Las variables de decisión deben adoptar valores no negativos.

Obtenga la solución óptima y valor óptimo para el modelo utilizando Solver de Excel. Comente brevemente las características de la solución obtenida.

La solución óptima se observa en las celdas con color amarillo de la imagen anterior. Notar que no se produce Combustible tipo 2 y que el Combustible 3 se produce a máxima capacidad. La utilidad o valor óptimo es de 285.509,26 euros.

Analice las siguientes variantes del problema, explicando los resultados:

Aumento de la disponibilidad de la Gasolina No Refinada Tipo 4 a 5.000 barriles por día.

En este caso el valor óptimo aumenta en 10.629,63 euros en relación al valor óptimo original. El Precio Sombra de la restricción de disponibilidad de barriles diarios para la gasolina 4 (disponible en el archivo para descarga al final de este artículo) es de aproximadamente 15,185 con un aumento permisible para el lado derecho de 3.662,5 barriles (diarios). Luego un incremento en la disponibilidad de gasolina 4 en 700 barriles diarios genera una utilidad adicional del 700*15,185=10.629,5 (la diferencia con los 10.629,63 euros es sólo por efecto de la aproximación de decimales).

Aumento de los costos de las gasolinas con un octanaje menor a 90 en un 10%.

En este caso no se observa un cambio en la solución óptima en comparación al escenario inicial, no obstante las utilidades se ven reducidas dado el aumento en el costo de las gasolinas 1 y 2 (aquellas que tienen un octanaje inferior a 90 puntos).

Aumento de la demanda del Combustible 3 en 2.000 barriles diarios.

Este caso representa una merma en cuanto a las utilidades al ser más restrictivo que el problema original. Notar que ahora no se asignan gasolinas para venta directa y que también disminuye la cantidad de barriles diarios a fabricar del Combustible 1, llegado a 3.450.

¿Quieres tener la resolución en Solver de Excel de este modelo de optimización?

[sociallocker]Problema Refinación de Combustibles[/sociallocker]

Análisis de Sensibilidad (Método Gráfico)

El Análisis de Sensibilidad en Programación Lineal permite analizar el impacto en los resultados del modelo (solución óptima y valor óptimo) en aquellos casos donde uno o varios parámetros sufren modificaciones en relación a sus valores originales, sin la necesidad de resolver nuevamente el problema (sin reoptimizar). En dicho contexto en el siguiente artículo presentamos un ejemplo de dicho análisis para un problema de optimización lineal que considera 2 variables de decisión.

Ejemplo Análisis de Sensibilidad (Método Gráfico)

Un productor tabaquero posee 85 hectáreas (ha) de terreno para plantar dos variedades de tabacos Virginia y Procesado. La variedad Virginia tiene un ingreso de 9.600 USD/ha y necesita 3 horas/ha de uso de maquinaria y 80 horas/ha de mano de obra. Además, el Estado limita su explotación a 30 ha como máximo. La variedad Procesado tiene un ingreso de 7.500 USD/ha y utiliza 2 horas/ha de uso de maquinaria y 60 horas/ha de mano de obra. La cooperativa local le ha asignado un máximo de 190 horas de uso de maquinaria y solo se dispone de 5.420 horas de mano de obra a 12 USD/hora.

Formule y resuelva gráficamente un modelo de Programación Lineal que permita determinar cuánto se debe plantar de cada variedad de tabaco de manera de maximizar la utilidad total.

En primer lugar definimos el modelo de optimización para este problema. Esto consiste en identificar las variables de decisión, función objetivo y restricciones. Detalle de este procedimiento aplicado a problemas de 2 variables puede ser consultado en el artículo Programación Lineal (Método Gráfico).

Variables de Decisión:

X₁ = Número de Ha a plantar de la variedad Virginia
X₂ = Número de Ha a plantar de la variedad Procesado

Función Objetivo:

Maximizar (9.600 – 960)X₁ + (7.500 – 720)X₂ = 8.640X₁ + 6.780X₂

Restricciones:

X₁ ≤ 30
X₁ + X₂ ≤ 85
3X₁ + 2X₂ ≤ 190
80X₁ + 60X₂ ≤ 5.420
X1, X2 ≥ 0

Una representación gráfica del problema para el productor de tabaco se puede realizar a través del software Geogebra:

Sabemos según el Teorema Fundamental de la Programación Lineal que en caso de existir solución óptima ésta se encontrará en un vértice o en un tramo en la frontera del dominio de soluciones factibles (en el ejemplo área achurada en color verde). Adicionalmente podemos apreciar que no es tan evidente que el vértice C reporte una mayor utilidad en la función objetivo que el vértice D, por lo cual, inspeccionaremos ambos puntos.

En el caso del vértice C éste se encuentra en la intersección de las restricciones 2 y 4. La coordenada respectiva se obtiene al resolver el siguiente sistema de ecuaciones:

X₁ + X₂ = 85
80X₁ + 60X₂ = 5.420

De donde X₁=16 y X₂=69, lo cual reporta un valor en la función objetivo de V(P)=8.640*(16)+6.780(69)=606.060.

Análogamente en el caso del vértice D las restricciones activas son 3 y 4:

3X₁ + 2X₂ = 190
80X₁ + 60X₂ = 5.420

Luego de resolver el sistema lineal anterior se obtiene X₁=28 y X₂=53, lo cual reporta un valor en la función objetivo de V(P)=8.640*(28)+6.780(53)=601.260.

En consecuencia la solución óptima del problema es X₁=16 y X₂=69, con valor óptimo V(P)=8.640*(16)+6.780(69)=606.060.

Una vez resuelto el escenario original a continuación se presentan algunos análisis adicionales que representan por separado modificaciones en los coeficientes de la función objetivo y restricciones del problema.

Intervalo Variación Coeficiente Función Objetivo

Determine cuánto podría variar la utilidad por hectárea del tabaco Virginia, manteniendo constante la utilidad por hectárea del tabaco procesado, de forma que la actual solución óptima no cambie. Para este caso determine el intervalo de variación de la utilidad total.

Sea en términos generales la función objetivo Z=C₁X₁+C₂X₂, donde inicialmente en el ejemplo C₁=8.640 y C₂=6.780. La pendiente de las curvas de nivel de la función objetivo es -C₁/C₂. De este modo se conserva la actual solución óptima (vértice C) en la medida que:

$-\frac{4}{3}\leq-\frac{C_{1}}{C_{2}}\leq -1$
$\frac{4}{3}\geq \frac{C_{1}}{C_{2}}\geq 1$
$\frac{4}{3}\geq \frac{C_{1}}{6.780}\geq 1$
$9.040\geq C_{1}\geq 6.780$

En este caso la utilidad por hectárea del tabaco Virginia puede variar entre 6.780 USD y 9.040 USD, de tal forma que el actual nivel de producción (solución óptima) sería el mismo. Lo anterior permite concluir que el intervalo de variación para la utilidad total será $576.300\leq Z\leq 612.460$ .

Precio Sombra (Método Gráfico)

Si se pudiese contratar más mano de obra disponible en el mercado, ¿Cuántas horas de mano de obra en total estaría dispuesto a utilizar? ¿Cuál sería el aporte adicional de esas horas extras que utilizaría en términos monetarios? Responda lo anterior utilizando el concepto de Precio Sombra.

Para calcular gráficamente el precio sombra necesitamos identificar la máxima y mínima variación para el lado derecho de la restricción de mano de obra que permita garantizar que se conserva la actual base óptima (restricciones activas originales). En este sentido en el caso de aumentar el lado derecho de dicha restricción la solución óptima podrá ser encontrada manteniendo las restricciones activas (e incorporando una adicional) hasta la coordenada (20,65) que es donde se interceptan la segunda y tercera restricción. En el caso de disminuir la disponibilidad de horas en mano de obra se mantiene la base óptima hasta el vértice B cuya coordenada es (0,85). De esta forma se obtiene el precio sombra de la siguiente forma:

En consecuencia el lado derecho de la restricción 4 (disponibilidad de mano de obra) puede variar entre [5.100, 5.500] y se conservan las actuales restricciones activas. Adicionalmente dado que en el óptimo actual se utilizan 5.420 horas de mano de obra se deben contratar 80 horas adicionales (de modo de alcanzar las 5.500 horas). Luego, la variación de 80 horas adicionales implicaría un aumento en la utilidad total de 80*USD93=7.440USD.

Cálculo del Intervalo de Variación del Lado Derecho que conserva la Base Óptima

Una vez concluidas las iteraciones del Método Simplex y en el caso de alcanzar una solución básica factible óptima, puede resultar de interés determinar un intervalo de variación para un parámetro del vector de los lados derechos de las restricciones que permita conservar la geometría del problema. Esto implica que se conservan las restricciones activas originales en el nuevo escenario (es decir, se mantiene la base óptima) que se genera a partir de la modificación (individual) de un parámetro o coeficiente del lado derecho. Para ilustrar el resultado anterior consideremos el siguiente modelo de Programación Lineal.

Luego de llevar a la forma estándar el modelo anterior agregando $x_{3}$ , $x_{4}$ y $x_{5}$ como las variables de holgura de las restricciones 1, 2 y 3, respectivamente, y aplicar las iteraciones necesarias del Método Simplex, se alcanza la siguiente tabla final (óptima):

La solución óptima es $x_{1}=15$ y $x_{2}=40$ con valor óptimo $V(P)=615$ . El valor de las variables de holgura en el óptimo $x_{3}$ , $x_{4}$ y $x_{5}$ es 0, 0 y 20, respectivamente. Luego se puede concluir que la solución óptima del problema se alcanza con las restricciones 1 y 2 activas (notar que sus respectivas holguras con variables no básicas en el óptimo) y la base actual esta conformada por las variables $x_{1}$ , $x_{2}$ y $x_{5}$ .

Sabemos adicionalmente que, por ejemplo, el costo reducido de la variable de holgura $x_{3}$ representa el precio sombra asociado a la primera restricción ( $\pi_{1}=1/2$ ). No obstante desconocemos en qué intervalo puede variar el parámetro del lado derecho de la restricción 1 (actualmente $b_{1}=180$ ) de modo que se conserve la base óptima y por tanto nos permita hacer un correcto uso de la información del precio sombra.

Para ello se propone la siguiente fórmula que permite encontrar el intervalo de variación para un lado derecho que conserva la base óptima:

Max {-bj/yij con yij>0} <= D <= Min {-bj/yij con yij<0}

Por ejemplo determinemos el intervalo para el parámetro $b_{1}$ :

En consecuencia $b_{1}$ puede disminuir en 30 unidades y aumentar en 15 unidades y se conserva la base óptima. Es decir, si $b_{1}\epsilon [150,195]$ se mantiene la base óptima.

El resultado anterior se puede corroborar gráficamente. La solución óptima se encuentra en el vértice C donde las restricciones 1 y 2 son activas (notar la curva de nivel que pasa por el vértice óptimo es la línea punteada de color azul). Si para el lado derecho de la restricción 1 consideramos $b_{1}=150$ se obtiene la línea de color verde y para $b_{1}=195$ la línea de color rojo. En estos casos si bien se modifica el dominio de soluciones factibles, la solución óptima conserva las actuales restricciones activas (y por ende cuando $b_{1}$ adopta un valor fuera de este intervalo cambia la geometría del problema o base óptima).

Esto es consistente con el Informe de Confidencialidad de Solver. En particular el reporte de restricciones donde se aprecia el aumento y reducción permisible que conserva la actual base óptima:

Por ejemplo, ¿cuál es el nuevo valor óptimo si el lado derecho de la restricción 1 ahora es $b_{1}=190$ ?. Como $b_{1}=190\epsilon[150,195]$ , entonces $V(P)=615+\Delta b_{1}\pi _{1}=615+(190-180)*(1/2)=620$ . ¿Cuál es la nueva solución óptima?. Como sabemos que se conservan las restricciones activas en el óptimo para la variación propuesta, la solución óptima del nuevo escenario se obtiene simplemente resolviendo el siguiente sistema de ecuaciones (notar que la restricción 1 y 2 se conservan activas):

De donde $x_{1}=20$ y $x_{2}=110/3$ , que al evaluar en la función objetivo se obtiene: $V(P)=9*(20)+12*(110/3)=620$ corroborando el resultado anterior. Dejamos al lector el desafío de aplicar los conceptos presentados en este articulo para encontrar un intervalo para $b_{2}$ y $b_{3}$ que conserve la base óptima.

Qué significa un Precio Sombra igual a Cero en Programación Lineal

Según hemos abordado en artículos anteriores el Precio Sombra de una restricción representa la tasa de cambio del valor óptimo ante una modificación marginal del lado derecho de una restricción. Se entiende por «marginal» aquella modificación que no cambia la geometría del problema, es decir, que la nueva solución óptima se puede encontrar a través de la resolución del sistema de ecuaciones al que da origen las restricciones activas originales (previa actualización del parámetro que estamos modificando). En este contexto el precio sombra puede ser un valor positivo, negativo o cero y en particular nos referiremos a este último caso en este artículo.

Consideremos el siguiente modelo de Programación Lineal en 2 variables:

El problema anterior lo podemos resolver gráficamente utilizando Geogebra, que da origen a un problema con infinitas soluciones óptimas en el tramo de recta que une los vértices B y C y que se puede denotar de forma general por: (X,Y)=λ(0,60)+(1-λ)(10,45) con λ en el intervalo entre [0,1]. El valor óptimo en consecuencia es V(P)=1.200.

¿Cuáles son las restricciones activas en el óptimo?. Por ejemplo si consideramos el vértice B (solución óptima) las restricciones activas son 3X+2Y<=120 y X>=0, sin embargo si seleccionamos el vértice C (también solución óptima) las restricciones activas son 5X+2Y<=140 y 3X+2Y<=120. Dado lo anterior ¿aumentará el valor óptimo si se dispone de unidades adicionales del recurso que representa el lado derecho de la restricción 5X+2Y<=140?.

Para ello buscaremos mantener activas las restricciones del vértice C identificando la máxima variación (aumentando el valor del lado derecho) que conserve las restricciones activas originales (esto genera un desplazamiento paralelo de la restricciones que hemos representado con la línea color punteada color rojo) lo cual se alcanza en la coordenada (X,Y)=(40,0). De forma análoga para determinar la mínima variación para el lado derecho desplazamos en un sentido de decrecimiento la restricción buscando conservar las restricciones activas originales hasta la coordenada (X,Y)=(0,60) (línea punteada color naranjo).

Evaluamos en la fórmula para el cálculo del precio sombra obteniendo lo siguiente:

Por tanto el precio sombra de la restricción 1 (5X+2Y<=140) es cero lo cual indica que si aumenta o disminuye el valor del parámetro que representa su lado derecho (actualmente b1=140) en el intervalo entre [120,200] no se verá afectado el valor óptimo del problema. Lo anterior es consistente con lo obtenido a través del informe de confidencialidad de restricciones de Solver de Excel:

En general un precio sombra igual a cero significa que la modificación del parámetro que representa el lado derecho de la respectiva restricción (en un intervalo que conserva la geometría del problema) no tiene un impacto en el valor óptimo del problema. Sin embargo, existen casos especiales como los problemas de Programación Lineal que admiten infinitas soluciones (como el descrito en este artículo) donde una restricción con precio sombra igual a cero puede ser activa en uno de los vértices óptimo (el caso más usual es que una restricción con precio sombra igual a cero no sea activa en el óptimo).