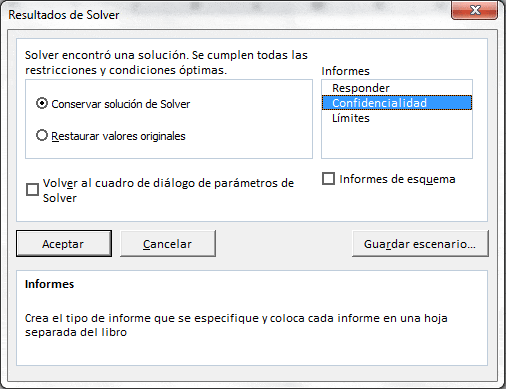
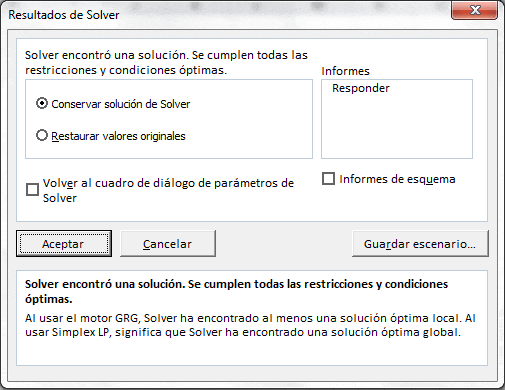
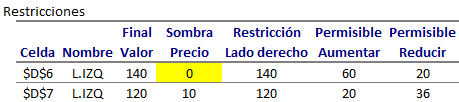
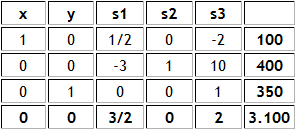
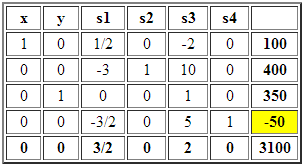
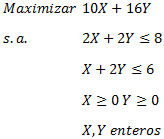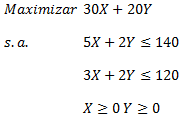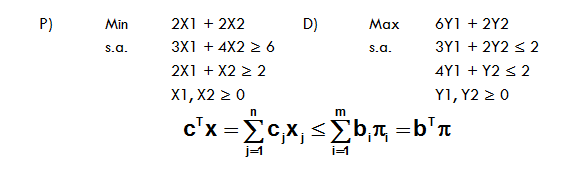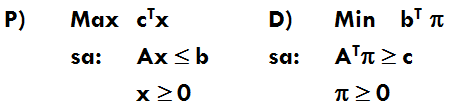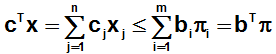Cuando resolvemos un modelo de Programación Lineal en Solver de Excel tenemos la posibilidad de generar una serie de informes de respuesta entre los cuales destaca el denominado «Confidencialidad» (o «Sensibilidad» en versiones de Excel anteriores) que resume los principales resultados relativos al análisis de sensibilidad. Lo anterior es fácilmente accesible en el módulo de Resultados de Solver en una interfaz similar como la que se presenta a continuación:
Sin embargo la opción de obtener el Informe de Confidencialidad no siempre está disponible. Para ello consideremos que nos interesa resolver el siguiente modelo de Programación Entera:
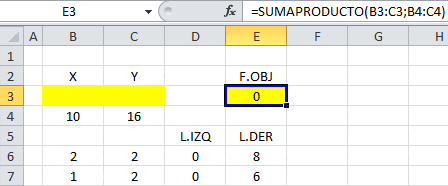
A continuación desarrollamos la implementación computacional según se muestra en la imagen a continuación:
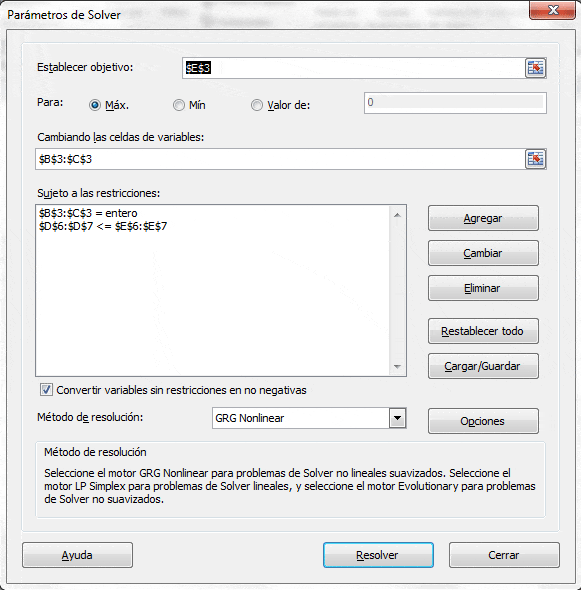
Se puede apreciar que la celda E3 es la fórmula de la función objetivo que representa la ponderación de los parámetros de la misma (10 y 16) por los valores que adquirirán las celdas que definiremos como variables de decisión (B3 y C3). Adicionalmente las celdas D6 y D7 también son fórmulas que considera la ponderación de los parámetros del lado izquierdo de las restricciones por las variables de decisión. Luego, se carga el modelo en Solver de Excel en la interfaz «Parámetros de Solver»:
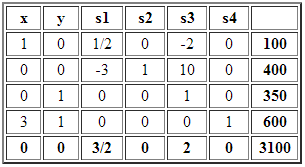
Para obtener los resultados sólo es necesario presionar «Resolver» donde se actualizará en la planilla los resultados con la solución óptima X=2 e Y=2 y valor óptimo V(PE)=52. Notar sin embargo que el informe de Confidencialidad ya no se encuentra disponible.
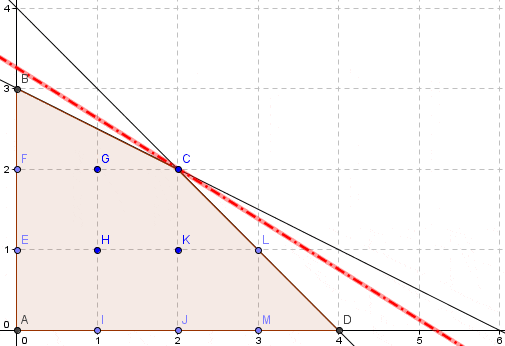
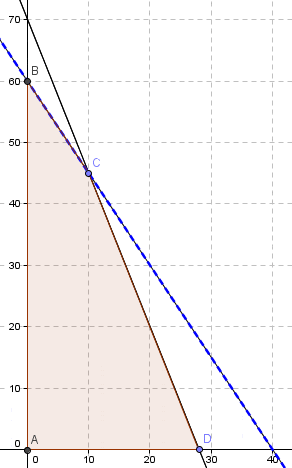
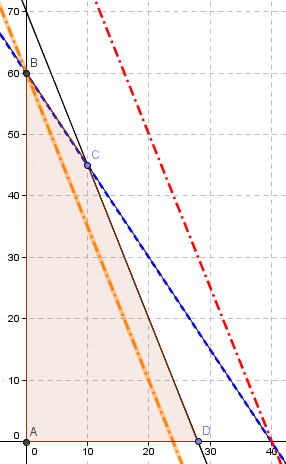
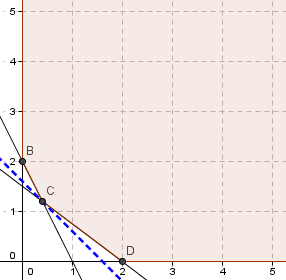
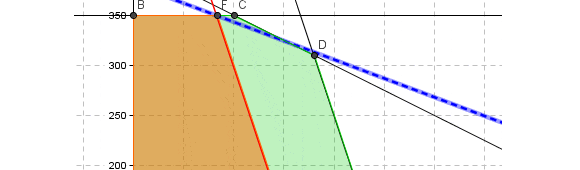
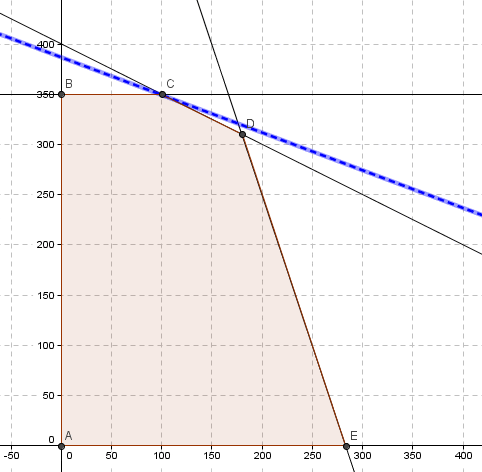
¿Por qué sucede ésto?. Básicamente por qué los informes de sensibilidad en Solver se pueden obtener si el problema que se implementa es de naturaleza continua (como lo que sucedería en este mismo problema si se omiten las condiciones de integralidad para las variables de decisión lo que daría lugar a un modelo de Programación Lineal). Por el contrario un modelo de Programación Entera como el que hemos utilizado en este artículo tiene un dominio de factibilidad discreto. Lo anterior queda en evidencia en la siguiente representación gráfica del problema realizada con Geogebra:
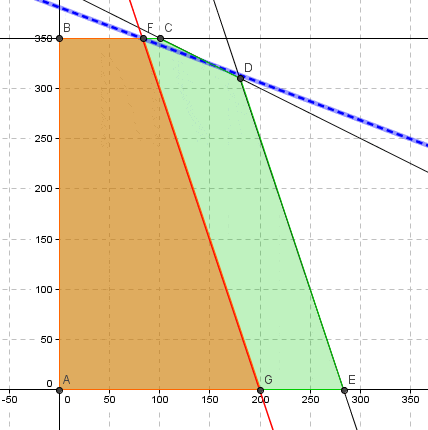
El dominio de factibilidad continuo del modelo de Programación Lineal (omitiendo las condiciones de enteros para las variables de decisión) corresponde al área achurada denotada por el polígono que tiene por los vértices A, B, C y D. En cuanto al modelo de Programación Entera el dominio de factibilidad es discreto y se puede enumerar, lo cual corresponde a las coordenadas que representan los puntos A, E, F, B, I, H, G, J, K, C, M, L y D. En este contexto se debe recordar que uno de los supuestos básicos de la Programación Lineal es la proporcionalidad el cual ya no es admisible cuando nos enfrentamos a un problema de Programación Entera.
En consecuencia, si en la utilización de Solver de Excel queremos analizar el impacto que tiene la modificación de los parámetros del modelo en la resolución de un modelo de Programación Entera (principalmente en lo que se refiere a la solución óptima y valor óptimo) se propone reoptimizar modificando la(s) celda(s) que sean necesarias y ejecutar el programa nuevamente.