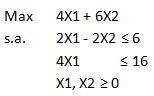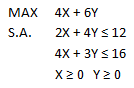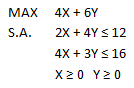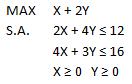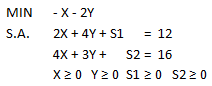resolución gráfica Archivos - Página 5 de 6

Cómo detectar que un Problema es No Acotado con el Método Simplex

El Método Simplex es un algoritmo que nos permite resolver modelos de Programación Lineal que en ciertas ocasiones permite identificar casos excepcionales como infinitas soluciones óptimas o que el problema es no acotado. En este contexto el Método Simplex rescata las condiciones establecidas en el Teorema Fundamental de la Programación Lineal.

En la aplicación del Método Simplex, un problema no acotado se detecta cuando en una iteración cualquiera existe una variable no básica con costo reducido negativo y todos los elementos en la columna de dicha variable son negativos o cero. Es decir, no se puede seleccionar un pivote para determinar la variable que debe dejar la base.

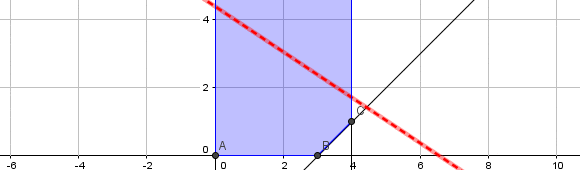
Consideremos el siguiente modelo de Programación Lineal:

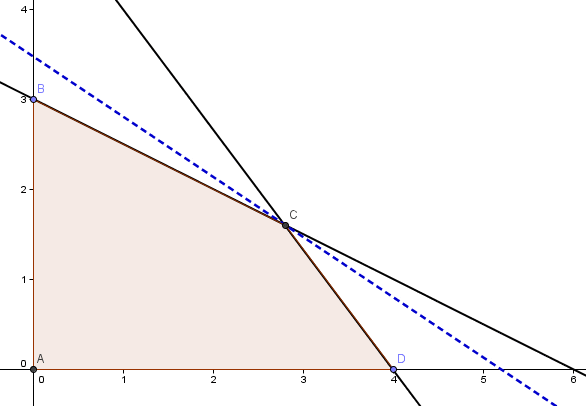
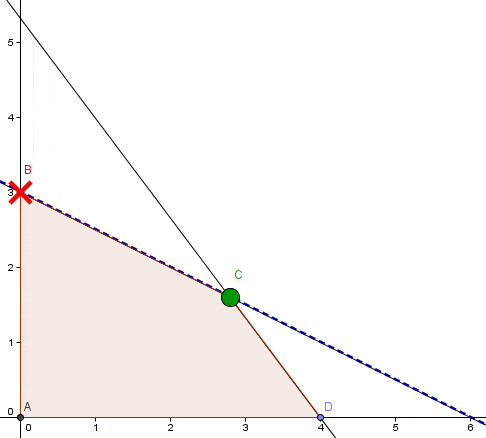
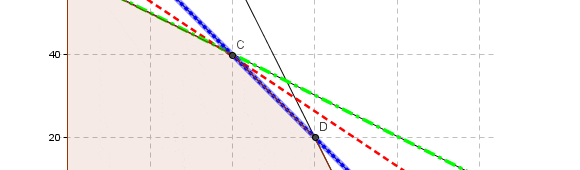
Si resolvemos gráficamente dicho modelo nos podemos percatar que éste es no acotado. Notar que el dominio de soluciones factibles (área sombreada o achurada) es no acotado dado que crece indefinidamente en la dirección de la variable X2.

Las curvas de nivel de la función objetivo crecen a su mayor tasa en la dirección del vector gradiente $\triangledown f(X_{1},X_{2})=(4,6)$ lo que indica que se podría desplazar indefinidamente en esa dirección y siempre interceptar el dominio de soluciones factibles.

¿Cómo podemos detectar esta situación (Problema No Acotado? utilizando el Método Simplex?

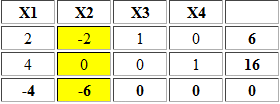
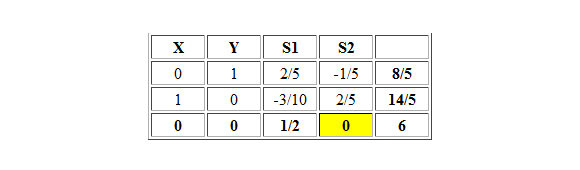
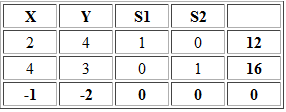
Para ello llevamos el modelo a su forma estándar, agregando X3 y X4 como variables de holgura de la restricción 1 y 2, respectivamente. Lo anterior define la siguiente tabla inicial del método:

Notar que X2 es la variable no básica con el costo reducido más negativo y siguiendo ese criterio debería ser aquella que ingresamos a la base. Sin embargo, no es factible hacer el criterio de factibilidad o mínimo cuociente debido a que los elementos en la columna de X2 son negativos o cero. En esta instancia ya se puede afirmar que el problema es no acotado.

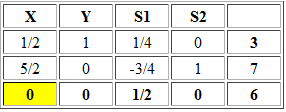
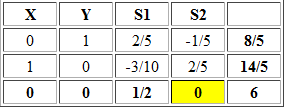
Observación: Se puede verificar que si seleccionamos X1 como la variable que entra a la base y se aplica una iteración del Método Simplex se llegara a una conclusión similar a la presentada anteriormente.

Diferencias entre la Programación No Lineal y la Programación Lineal

El supuesto de la proporcionalidad de la Programación Lineal (PL) no siempre es adecuado para representar de buena forma situaciones de naturaleza real que requieren de un modelo de optimización como apoyo para el proceso de toma de decisiones.

Cabe señalar que un modelo de Programación No Lineal (PNL) es aquel donde la función objetivo y/o las restricciones son funciones no lineales de las variables de decisión.

En este sentido la Programación No Lineal permite enfrentar una serie de aplicaciones prácticas que requieren una representación a través de funciones no lineales.

Algunos casos característicos de la Programación No Lineal son los problemas de minimización de distancia, economías o deseconomías de escala, carteras de inversión, ajuste de curva, entre otros.

En general cuando formulamos un modelo de optimización no lineal esperamos que éste sea más representativo de una situación real en comparación a un modelo lineal, sin embargo, a la vez asumimos que es probable que la complejidad de la resolución aumente. Por ello quien formule un modelo debe equilibrar la representatividad del mismo con la dificultad de la resolución.

A continuación presentaremos dos modelos de optimización que comparten las mismas restricciones (que asumiremos por simplicidad que son funciones lineales) y se diferencian por la naturaleza de la función objetivo (lineal y no lineal, respectivamente). Estos ejemplos nos ayudarán a explicar algunas diferencias entre la Programación Lineal y Programación No Lineal:

Si Resolvemos Gráficamente el modelo de Programación Lineal obtenemos la solución óptima en el vértice C (X=14/5 Y=8/5 y valor óptimo V(P)=20,8) lo cual corresponde a una Solución Básica Factible Óptima.

En efecto, una de las propiedades básicas de la Programación Lineal es que cuando un modelo admite solución, ésta se encontrará en un vértice (o tramo frontera en el caso Infinitas Soluciones Óptimas) del dominio de soluciones factibles. (Recomendación: Ver Teorema Fundamental de la Programación Lineal).

En cuanto a la resolución del modelo de Programación No Lineal, las curvas de nivel de la función objetivo no lineal tiene la forma de circunferencias concéntricas desde la coordenada (X,Y)=(2,4). Como la función objetivo es de minimización, buscamos la circunferencias de menor radio (o diámetro) que intercepte por primera vez el dominio de soluciones factibles. Esto se alcanza en (X,Y)=(1,2,2,4).

El resultado anterior se puede verificar mediante la aplicación de las condiciones de optimalidad que establece el Teorema de Karush-Kuhn-Tucker (KKT) al ser éste un problema de Programación No Lineal restringido.

Conclusión: Si un modelo de Programación No Lineal admite solución óptima, ésta se puede encontrar en cualquier punto del dominio de soluciones factibles.

Por ejemplo, si la función objetivo estuviese centrada en la coordenada (X,Y)=(2,1) ésta ya sería la solución óptima del problema. Notar que esta situación (solución en un punto interno del dominio factible) NO sería posible en la resolución de un modelo de Programación Lineal.

En los artículos de la categoría de Programación No Lineal analizamos algunos algoritmos especializados para la resolución de modelos no lineales como también herramientas computacionales para enfrentar este tipo de problemas.

Interpretación del Informe de Sensibilidad de Celdas Cambiantes (Solver)

Cuando Resolvemos un modelo de Programación Lineal con Solver de Excel utilizamos una estimación de los parámetros (constantes) los cuales generalmente hacen referencia a disponibilidad de recursos, precios, costos, etc. En este contexto nos interesa simular el impacto en los resultados ante variaciones marginales de dichos parámetros sin la necesidad de resolver un nuevo modelo de optimización.

Este objetivo se puede alcanzar a través de los Informes de Sensibilidad de Solver los cuales se pueden generar una vez resuelto un escenario base para un modelo de optimización lineal, seleccionando la opción “Sensibilidad” (o Confidencialidad en versiones recientes de Office) según se muestra a continuación:

El siguiente análisis explica cómo interpretar el Informe de Sensibilidad de Celdas Cambiantes de Solver para el siguiente modelo de Programación Lineal:

Con solución óptima X=14/5 Y=8/5 y valor óptimo V(P)=20,8. El Informe de Celdas Cambiantes corresponde a:

Notar que en la última columna se ha marcado con color rojo la palabra Aumento que debiese decir Disminución (este tipo de error se observa generalmente en las versiones más antiguas de Office).

El Informe de Sensibilidad de Celdas Cambiantes nos indica el intervalo de variación para cada parámetro de la función objetivo que permite mantener la actual solución óptima (asumiendo que el resto de los parámetros permanece constante).

Por ejemplo, el coeficiente que actualmente pondera a la variable X en la función objetivo de maximización es 4. El aumento permisible de 4 nos indica que el actual parámetro podría aumentar en dicha magnitud y la solución óptima actual se mantendría.

Análogamente se podría disminuir en 1 unidad (disminución permisible) y se conserva la solución actual.

En conclusión, el Intervalo de Variación para el parámetro que pondera a la variable X en la función objetivo que conserva la actual solución óptima es entre [3,8].

Siguiendo un procedimiento similar se puede demostrar que el intervalo de variación para el parámetro asociado a la variable Y en la función objetivo que conserva la actual solución óptima es entre [3,8] (sólo es una coincidencia que sean los mismos intervalos para cada parámetro).

Por ejemplo, un cambio en uno de los parámetros de la función objetivo afecta la pendiente de ésta (curvas de nivel) que en la medida que se encuentre en el intervalo de variación previamente determinado mantendrá al vértice C como solución óptima del problema.

Una forma sencilla de corroborar estos resultados es mediante el Método Gráfico en Programación Lineal. Adicionalmente en el artículo Análisis de Sensibilidad Método Gráfico se detalla el procedimiento para obtener los intervalos de variación para los parámetros tanto en la función objetivo como en las restricciones del problema. Recomendamos revisar ambos artículos de modo de favorecer la comprensión de este tipo de análisis.

Cómo detectar Infinitas Soluciones con el Método Simplex

Una de las posibilidades a las que nos podemos enfrentar cuando resolvemos un modelo de Programación Lineal a través del Método Simplex es el caso de múltiples o infinitas soluciones óptimas.

Esto significa que existe un tramo de soluciones factibles que reportan idéntico valor para la función objetivo y que no es posible mejorar.

En este contexto si luego de aplicar las iteraciones que resulten necesarias por el Método Simplex a un modelo de Programación Lineal (tabla óptima o tableau óptimo) se verifica que una variable no básica óptima tiene costo reducido igual a cero, esto permitirá afirmar que estamos ante el caso de infinitas soluciones.

Ejemplo Infinitas Soluciones Óptimas Método Simplex

Consideremos el siguiente modelo de Programación Lineal:

Llevamos el modelo a su forma estándar para proceder con la aplicación del Método Simplex, con S1 y S2 como variables de holgura de la restricción 1 y 2, respectivamente.

La tabla inicial con S1 y S2 como variables básicas iniciales es:

Y entra a la base. Luego para determinar la variable que deja la base utilizamos el criterio del mínimo cuociente: Min {12/4 ; 16/3} = 3 ==> S1 deja la base. Con esta información actualizamos la tabla realizando operaciones fila:

Luego de una iteración encontramos la solución óptima, donde Y y S2 son variables básicas. La solución básica factible óptima es X=0 Y=3 S1=0 S2=7. El valor óptimo es V(P)=6.

Notar que X (variable no básica) tiene costo reducido igual a cero lo que determina la existencia de múltiples o infinitas soluciones óptimas, de modo que la solución actual es uno de los vértices óptimos.

El siguiente diagrama muestra la Resolución Gráfica del problema con el software Geogebra donde la solución óptima que hemos encontrado en la aplicación del Método Simplex corresponde al vértice B.

Notar que la línea punteada de color azul corresponde a una curva de nivel de la función objetivo que tiene la misma pendiente que la restricción 1 (pendiente -1/2).

¿Cómo podemos obtener el vértice C que es solución óptima a través del Método Simplex? Una alternativa sería forzando la entrada a la base de la variable X en la tabla óptima. Luego calculamos cuál de las actuales variables básicas deja la base según el criterio del mínimo cuociente: Min {3/1/2 ; 7/5/2} = 14/5 ==> S2 deja la base. Actualizando la tabla obtenemos:

La nueva solución óptima (con idéntico valor óptimo) es X=14/5 Y=8/5 S1=0 S2=0, que corresponde al vértice C en el gráfico anterior. Ahora la variable no básica S2 tiene costo reducido igual a cero en la tabla óptima que señala el caso de múltiples soluciones óptimas (en este ejemplo el tramo BC).

Cómo calcular Gráficamente el Precio Sombra de una Restricción

El Precio Sombra de una restricción en Programación Lineal indica cuánto cambia el valor de la función objetivo (óptimo) ante una variación marginal del lado derecho de una restricción. Se asume que el resto de los parámetros del modelo permanecen constantes. De antemano es conveniente señalar que el Precio Sombra puede ser positivo, cero o negativo y en el Blog iremos discutiendo estos distintos escenarios.

Para obtener los Informes de Sensibilidad de un modelo de Programación Lineal se puede hacer uso de herramientas computacionales como Solver de Excel, sin embargo, en esta oportunidad nos enfocaremos en el cálculo del precio sombra de una restricción en forma gráfica, lo que nos ayudará más adelante a entender los conceptos que fundamentan los resultados de Solver.

Cálculo del Precio Sombra de una Restricción con el Método Gráfico

A continuación calcularemos el precio sombra de una restricción del siguiente modelo de Programación Lineal:

La solución óptima de este modelo es X=100 e Y=350 con valor óptimo V(P)=3.100 según su resolución gráfica con Geogebra o su resolución con Solver de Excel. El siguiente diagrama muestra la solución óptima obtenida gráficamente en el vértice C, que corresponde a la intersección de la restricción 1 (R1: color rojo) y la restricción 3 (R3: color gris), siendo ésta una solución básica factible óptima.

Supongamos que deseamos saber cuánto cambiará el valor óptimo (respecto a su valor actual) si aumenta en una unidad el lado derecho de la restricción 1 pero sin resolver nuevamente el problema. El precio sombra nos permite dar respuesta a dicha interrogante y permite anticipar el nuevo valor óptimo ante una variación marginal del lado derecho de una restricción.

Un variación marginal de un lado derecho implica que la nueva solución óptima se seguirá encontrando con las actuales restricciones activas, es decir, aquellas que se cumplen en igualdad en el óptimo (esto es se conserva la base óptima).

En el caso de la restricción 1 si aumentamos su lado derecho, ésta se desplazará en forma paralela hacia arriba. Si buscamos garantizar que la nueva solución óptima aún se encontrará con R1 y R3 activas llegaremos al vértice donde actualmente se interceptan la R2 y R3 que corresponde a la coordenada X=166,67 e Y=350 (ésta será la máxima variación).

En forma análoga si disminuimos el lado derecho de la restricción 1 y buscamos mantener R1 y R3 activas en el nuevo óptimo, el último punto donde se garantiza esto es el vértice B cuyas coordenadas son X=0 e Y=350 (ésta será la menor variación). Con esta información calculamos el precio sombra de la restricción 1:

Este precio sombra es válido si el lado derecho de la restricción 1 (actualmente b1=1.600) varía entre [1.400,1.733,33]. Por ejemplo, si el lado derecho de R1 aumenta de 1.600 a 1.700 el nuevo valor óptimo será V(P)=3.100+100*1,5=3.250. Análogamente si el lado derecho de R1 disminuye de 1.600 a 1.550 el nuevo valor óptimo será V(P)=3.100-50*1,5=3.025. (Se recomienda corroborar estos resultados gráficamente con TORA o IORTutorial). Notar que si la variación del lado derecho de la restricción 1 está por fuera del intervalo [1.400,1.733,33], no se puede utilizar el precio sombra para predecir cuál será el nuevo valor óptimo.

En un próximo análisis complementaremos el cálculo del precio sombra de las restricciones 2 y 3 en conjunto con otros Análisis de Sensibilidad en la resolución de modelos de programación lineal. Hasta entonces!