Minientrada archivos - Página 2 de 8 - Gestión de Operaciones

Ejemplo del Plan de Requerimientos de Materiales (MRP)

El Plan de Requerimientos de Materiales o simplemente MRP por sus siglas en inglés (Material Requirements Planning) es una metodología que permite administrar el inventario y planificar pedidos de partes y piezas con demanda dependiente.

En la actualidad el MRP resulta ser un módulo indispensable para la gestión de los recursos de las empresas de manufactura y son parte fundamental de las prestaciones de los más prestigiosos softwares ERP (Enterprise Resource Planning) disponibles en el mercado (destacándose entre ellos SAP).

En el siguiente artículo encontrarás a través de un ejemplo sencillo, explicado con detalle, cómo realizar un Plan de Requerimientos de Materiales (MRP) y cuáles son los elementos necesarios para su construcción. Para una correcta comprensión introduciremos algunos conceptos que te recomendamos leer detenidamente.

En primer lugar se afirma que un producto tiene demanda dependiente en la medida que su demanda se puede derivar de un producto de categoría superior.

Ejemplo N°1: las plantillas, cuero, cordones, etc, son partes de demanda dependiente, basadas en la demanda de zapatos (demanda independiente).

Ejemplo N°2: si una empresa vende 1.000 triciclos, entonces se van a necesitar 1.000 ruedas delanteras y 2.000 ruedas traseras (más pequeñas). Este tipo de demanda interna no necesita un pronóstico, sino sólo una tabulación (demanda dependiente). Por otra parte la cantidad de triciclos que la empresa podría vender es la demanda independiente.

En este contexto, una empresa que vende un producto final (con demanda independiente) está interesada en qué, cuánto y cuándo ordenar de las distintas partes y piezas que permiten la producción de dicho producto final. Esta Planeación de Requerimientos de Materiales es crítica dado que permitirá alcanzar las metas de producción en tiempo y cantidad de lo planificado previamente en un plan maestro de producción.

Para llevar a cabo un Plan de Requerimientos de Materiales (MRP) se necesitan 3 elementos:

Plan Maestro de la Producción (PMP)
Estructura del Producto, Lista de Materiales o Bill of Materials (BOM)
Registro del Inventario (IRF)

El Plan Maestro de la Producción (PMP) establece las necesidades en cantidad y tiempo del producto final o con demanda independiente.

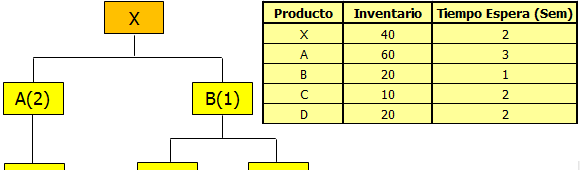
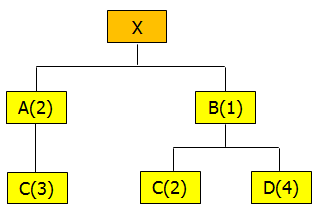
Por otra parte la estructura del producto o Bill of Materials (BOM) detalla cuántas partes y piezas se necesitan para obtener una unidad de producto final y cómo dicho producto se compone. Generalmente se utiliza una representación gráfica para el BOM como la de la siguiente imagen:

Por ejemplo, para cada unidad de X (producto final con demanda independiente) se necesitan 2 unidades de la pieza A (producto con demanda dependiente). Análogamente, por cada unidad de la pieza A se necesitan 3 unidades de la pieza C.

Así también, un típico juego de Lego viene con un instructivo que detalla la cantidad de piezas componentes del producto (juego) final y el orden en el cual se deben ensamblar. De este modo si hemos armado un juego de Lego ya tenemos una idea intuitiva de lo que consiste un MRP.

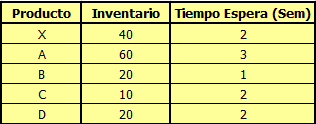
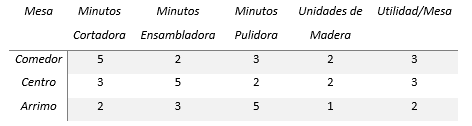
Finalmente necesitamos el Registro del Inventario (Inventory Record File o IRF) (tanto para productos con demanda dependiente e independiente) que contiene la información del inventario disponible y el tiempo de espera (o lead time) asociado a cada producto. Un ejemplo del IRF es el siguiente:

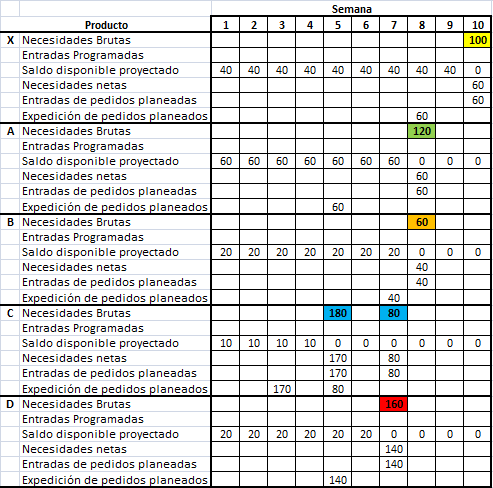
Arbitrariamente vamos a considerar que necesitamos 100 unidades el producto X en la semana 10. Toda esta información nos permitirá desarrollar el Plan de Requerimientos de Materiales, el cual se resume a continuación:

Ejemplo del Plan de Requerimientos de Materiales

La forma usual de poder completar la información del Plan de Requerimientos de Materiales (MRP) es desde el producto de categoría superior, en este caso, el Producto X. Para la semana 10 existe una necesidad bruta de este producto por 100 unidades, sin embargo, el inventario disponible (40 unidades) finalmente determina que sólo se necesiten 60 unidades adicionales. Como el tiempo de espera (lead time) para el Producto X es de 2 semanas, el pedido se debe realizar en la semana 8.

Posteriormente, por cada unidad del Producto X necesitamos 2 unidades del Producto A. Esto determina la necesidad bruta del Producto A en 120 unidades en la semana 8. Luego, como se dispone de un inventario de 60 unidades del producto A, la necesidad neta es sólo de 60 unidades, las cuales se piden con 3 semanas de antelación dado el tiempo de espera. Siguiendo el mismo procedimiento se determinan las necesidades netas del Producto B.

Es importante destacar el caso del Producto C, el cual depende tanto de A como B. Por cada unidad de A se necesitan 3 unidades de C (en este caso 180 unidades) y por cada unidad de B se necesitan 2 unidades de C (en este caso 80 unidades).

El procedimiento utilizado para desarrollar el Plan de Requerimientos de Materiales (MRP) es la política de lotificación Lote a Lote, es decir, cada vez que se necesitan unidades se piden éstas en forma exacta. Esta alternativa, sin embargo, NO garantiza los menores costos en la planificación, especialmente cuando los costos de emisión (generar un pedido) son relativamente superiores a los costos de almacenamiento (inventario).

Te recomendamos consultar al final de esta publicación los «Artículos Relacionados» donde podrás encontrar otros ejemplos aplicados de MRP utilizando distintas alternativas de políticas de lotificación (Costo Total Mínimo, Costo Unitario Mínimo, EOQ).

Instalación del Complemento Solver en Excel 2003

El complemento de Solver de Excel es una poderosa herramienta que permite resolver modelos de optimización utilizando una planilla de cálculo (Excel). En artículos anteriores hemos mostrado Cómo resolver Modelos de Programación Lineal utilizando Solver y algunas aplicaciones clásicas como el Problema de Transporte y Problema de la Dieta.

Las características de Solver han evolucionado en las distintas versiones de Office y en esta oportunidad mostraremos cómo activar este complemento en la versión del año 2003 y 2007. Para ello se deben seguir los siguientes pasos:

Paso 1: Abrir el programa Excel y en el menú de Herramientas seleccionar Complementos.

Paso 2: Seleccionar la opción Solver y luego Aceptar.

Paso 3: Puede ser necesario aprobar la ejecución del complemento como muestra la imagen a continuación. En este caso se debe seleccionar Sí

Paso 4: Una vez completada la activación de Solver el complemento estará disponible en el menú de Herramientas de Excel.

Una alternativa a Solver es el complemento de Excel OpenSolver el cual se puede descargar gratuitamente desde www.opensolver.org. En el artículo Cómo resolver un modelo de Programación Lineal con OpenSolver mostramos su utilización en un problema sencillo. Adicionalmente What’sBest! resulta ser otra excelente alternativa para Solver y desarrollado para Excel. En el siguiente tutorial detallamos cómo descargar e instalar What’sBest!.

Teorema de Holguras Complementarias: Dualidad en Programación Lineal

Uno de los teoremas principales en la Teoría de Dualidad en Programación Lineal es el Teorema de Holguras Complementarias.

El Teorema de Holguras Complementarias nos permite encontrar la solución óptima del Problema Dual cuando conocemos la solución óptima del Problema Primal (y viceversa) a través de la resolución de un sistema de ecuaciones conformado por las variables de decisión (primales y duales) y las restricciones (del modelo primal y dual).

La importancia de este teorema radica en que facilita la resolución de los modelos de optimización lineal, permitiendo a quién los resuelve buscar el modelo más sencillo para abordar (desde el punto de vista algorítmico) dado que de cualquier forma podrá obtener los resultados del modelo equivalente asociado (sea éste el modelo primal o dual).

Ejemplo Teorema de Holguras Complementarias

Consideremos el siguiente modelo de Programación Lineal (en adelante Primal) en 2 variables cuya solución óptima obtenida por el Método Gráfico es X=14/5 e Y=8/5 con valor óptimo V(P)=20,8.

El modelo Dual asociado al modelo primal es: (ante dudas de cómo pasar del problema primal al problema dual se recomienda revisar el artículo Relaciones de Dualidad en Programación Lineal (Cómo pasar de Primal a Dual))

Luego, el Teorema de Holguras Complementarias plantea las siguientes relaciones:

Como sabemos X=14/5 e Y=8/5 (Solución Básica Factible Óptima del modelo primal). Si reemplazamos estos valores de X e Y en la tercera y cuarta ecuación generamos un sistema de ecuaciones de 2×2 en términos de A y B cuya solución corresponde a A=6/5 y B=2/5 (solución óptima del modelo dual). Si posteriormente evaluamos en la función objetivo del problema dual dicha solución obtenemos: V(D)=12(6/5)+16(2/5)=20,8 que es similar al valor óptimo del problema primal (Teorema de Dualidad Fuerte).

Siendo A=6/5 y B=2/5 una solución factible para el problema dual, ésta es la solución optima de dicho problema.

Observaciones: Notar que la restricción 1 y 2 del problema primal son activas en el óptimo, es decir, se cumplen en igualdad. Esto permite descartar que A y B (variables duales asociadas a dichas restricciones) son iguales a cero. Si por ejemplo, la restricción 1 del modelo primal no fuese activa en el óptimo se podría afirmar que A es igual a cero en el dual.

Ejercicio Teorema de Holguras Complementarias en Programación Lineal

Una empresa que fabrica muebles desea estudiar la producción de varios tipos de mesas de madera. Las mesas a fabricar son mesas de comedor, de centro y de arrimo, las que deben ser procesadas por 3 tipos de máquinas, una cortadora, una ensambladora y una pulidora. Se dispone de a lo mas de 80 horas de trabajo en cada una de las máquinas y 2.000 unidades de madera. La siguiente tabla muestra los tiempos y la madera necesaria para la fabricación de cada mesa, así como la utilidad que reporta cada una de ellas.

Dadas las siguientes soluciones del Problema Primal S1=(900,100,0), S2=(176,496,656), S3=(200,400,550) y S4=(800,0,400). Determine mediante el Teorema de Holguras Complementarias si alguna de estas soluciones es óptima para el Problema Primal planteado.

Sea el Problema Primal el siguiente:

Variables de Decisión:

X1 : Cantidad de mesas de comedor a producir
X2 : Cantidad de mesas de centro a producir
X3 : Cantidad de mesas de arrimo a producir

Función Objetivo:

MAX Z = 3 X1 + 3 X2 + 2 X3

Restricciones:

5 X1 + 3 X2 + 2 X3 <= 4.800 (tiempo cortadora)
2 X1 + 5 X2 + 3 X3 <= 4.800 (tiempo ensambladora)
3 X1 + 2 X2 + 5 X3 <= 4.800 (tiempo pulidora)
2 X1 + 2 X2 + 1 X3 <= 2.000 (disponibilidad de madera)
X1>=0, X2>=0, X3>=0

Su correspondiente Problema Dual asociado es:

MIN W = 4.800 Y1 + 4.800 Y2 + 4.800 Y3 + 2.000 Y4
S.A.

5 Y1 + 2 Y2 + 3 Y3 + 2 Y4 >= 3
3 Y1 + 5 Y2 + 2 Y3 + 2 Y4 >= 3
2 Y1 + 3 Y2 + 5 Y3 + 1 Y4 >= 2
Y1>= 0, Y2>=0, Y3>=0, Y4>=0

A continuación verificamos la factibilidad de las soluciones propuestas para el Problema Primal:

S1=(900,100,0), V(S1)=3.000 Satisface todas las restricciones
S2=(176,496,656) V(S2)=3.328 Satisface todas las restricciones
S3=(200,400,550) V(S3)=2.900 Satisface todas las restricciones
S4=(800,0,400) V(S4)=3.200 Satisface todas las restricciones

Todas las soluciones satisfacen todas las restricciones por lo que son todas soluciones factibles. De ellas se escoge S2 ya que entrega la mayor utilidad para verificar si es solución óptima: X1=176, X2=496, X3=656.

En restricción (1) holgura X4 = 1.120
En restricción (2) holgura X5 = 0
En restricción (3) holgura X6 = 0
En restricción (4) holgura X7 = 0

De esta forma el Teorema de Holguras Complementarias permite obtener lo siguiente:

Que al ser reducido permite obtener un sistema de ecuaciones de 3×3:

2 Y2 + 3 Y3 + 2 Y4 = 3
5 Y2 + 2 Y3 + 2 Y4 = 3
3 Y2 + 5 Y3 + 1 Y4 = 2

Solución Problema Dual : Y1=0, Y2=1/25, Y3=3/25, Y4=32/25. Al evaluar la solución alcanzada en la función objetivo del dual se obtiene: W=4.800*0+4.800*1/25+4.800*3/25+2.000*32/25=3.328. Por el Teorema de Dualidad Fuerte W=Z por lo tanto S2 es solución óptima del Problema Dual.

Cómo resolver un modelo de Programación No Lineal con AMPL

La complejidad adicional que representan los modelos de Programación No Lineal en comparación a los modelos de Programación Lineal, justifica el desarrollo de algoritmos especializados que permitan abordar de forma más eficiente la resolución de este tipo de modelos.

En este contexto, uno de los lenguajes de programación matemática más conocidos y confiable para formular diversos modelos de optimización es AMPL (www.ampl.com). Su popularidad ha sido sustentada adicionalmente por el desarrollo de distintos algoritmos de resolución (o solvers) que son compatibles con AMPL y que permiten resolver modelos de Programación Lineal, Programación No Lineal, Programación Entera, entre otras.

Estos solvers han sido resultado del trabajo de prestigiosas universidades y centros de investigación, en algunos casos en conjunto con empresas de software. El servidor NEOS consolida esta información en Internet.

A continuación mostraremos cómo resolver un modelo de Programación No Lineal sencillo utilizando la versión estudiantil de AMPL y utilizando el solver de resolución MINOS versión 5.5. Para ello debemos descargar el archivo «amplcml.zip» a nuestro computador, descomprimir éste y luego ejecutar el archivo de nombre «ampl».

Consideremos el siguiente modelo de Programación No Lineal:

La sintaxis utilizada por AMPL es bastante intuitiva como se aprecia a continuación en la resolución del ejemplo:

var x1>=0; # definición de la variable x1 estableciendo condición de no negatividad.
var x2>=0; # definición de la variable x2 estableciendo condición de no negatividad.
minimize funcionobjetivo: (x1-2)^2+(x2-4)^2; # definición de la función objetivo. El nombre de la misma es arbitrario.
subject to restriccion1: 2*x1+4*x2<=12; # se define la inecuación correspondiente a la restricción 1.
subject to restriccion2: 4*x1+3*x2<=16; # se define la inecuación correspondiente a la restricción 2.
solve; # una vez implementado el modelo se ejecuta su resolución haciendo uso de MINOS 5.5 (opción por defecto)

La solución óptima es X1=1,2 y X2=2,4 con valor óptimo V(P)=3,2. (Puedes consultar aquí la Resolución Gráfica de este modelo). Adicionalmente se pueden corroborar los resultados a través de la aplicación de las condiciones de optimalidad de Karush-Kuhn-Tucker (KKT).

Congreso Optima 2011 sobre Investigación Operativa en Pucón Chile

Óptima 2011 es un congreso bienal organizado por el Instituto Chileno de Investigación Operativa (ICHIO) que tiene por objetivo la difusión de la Investigación Operativa (conocida también como Investigación de Operaciones) en Chile, a través de la presentación de trabajos, conferencias, sesiones de trabajos, entre otras.

El congreso Óptima se desarrolla cada 2 años y en esta oportunidad la Universidad encargada de su organización es la Universidad de la Frontera. Óptima 2011 se desarrollará entre el 26 y 29 de Octubre del año 2011 en la ciudad de Pucón (Novena Región de Chile) la cual se caracteriza por su belleza y ser uno de los lugares de atracción turística más importante del sur de Chile.

Invitamos cordialmente a nuestros lectores a informarse de los detalles del congreso en la página web que la Universidad de la Frontera ha dispuesto para dichos efectos. Óptima 2011.