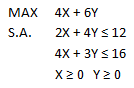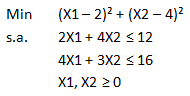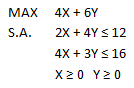Minientrada archivos - Página 3 de 8 - Gestión de Operaciones

Cómo reducir la duración de un Proyecto (Crashing) con WINQSB

Un aspecto relevante en todo Proyecto es lograr estimar el tiempo necesario para completar las distintas actividades que lo conforman. En artículos anteriores hemos analizado el Método de Ruta Crítica (CPM) y la Metodología PERT, asumiendo tiempos de actividades deterministas (fijos) y aleatorios (probabilísticos), respectivamente.

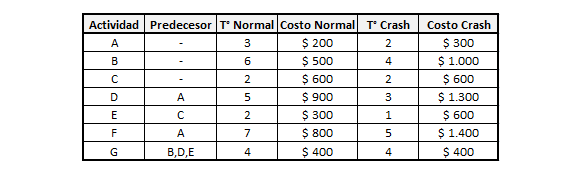
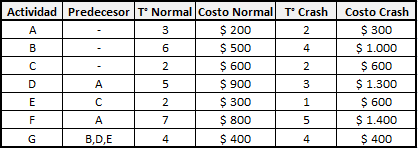
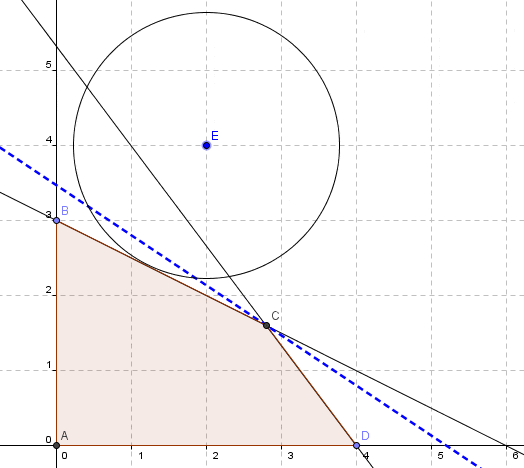
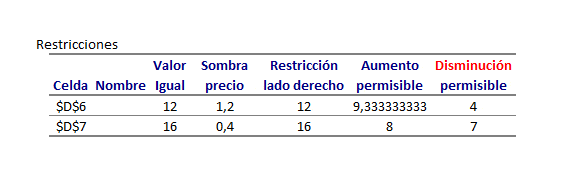
En esta oportunidad consideraremos un Proyecto que consta de 7 actividades y que en condiciones de tiempo normal tiene por Ruta Crítica a las actividades A-D-G con una duración total de 12 semanas:

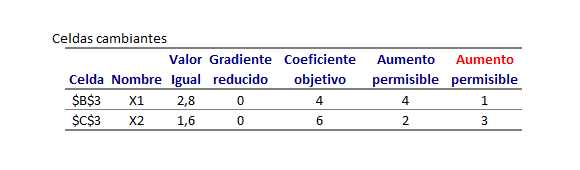
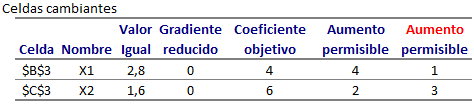
La tabla anterior incluye adicionalmente información sobre el costo normal de desarrollar las actividades en condiciones de tiempo normal y el tiempo crash que consiste el menor tiempo en el que se podría llevar a cabo la actividad en caso que se «apure».

En muchos proyectos existen actividades que podrían demorar menos si se invirtiera más recursos en ellas (costo crash), sin embargo, hay actividades que no son factibles de acortar (por ejemplo, podría ser el tiempo requerido para obtener un permiso por parte de una oficina del gobierno central, asunto que esta fuera del alcance del gerente del proyecto).

Por ejemplo, si quisiéramos reducir el tiempo de la actividad A de 3 a 2 semanas el costo incremental es de $100. Análogamente el costo de reducir el tiempo de la actividad B en 1 semana sería de $250 (se asume proporcionalidad).

El costo actual del proyecto es de $3.700 (suma de los valores de la columna «Costo Normal») para un tiempo estimado de 12 semanas (A-D-G Ruta Crítica).

Si queremos que el proyecto se demore menos de 12 semanas debemos estar dispuestos a asumir un costo monetario mayor. En este contexto el Análisis de Crashing (reducir la duración de un proyecto a un costo eficiente) resulta vital.

El siguiente tutorial muestra cómo reducir la duración de un proyecto utilizando el software WINQSB:

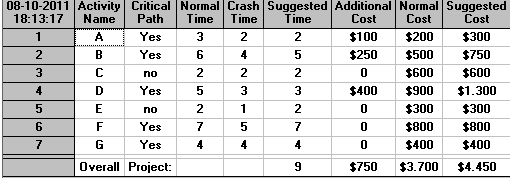
El menor tiempo en el cual se puede desarrollar el proyecto es 9 semanas con un costo total de $4.450. Para ello se reduce el tiempo de las actividades A y B en 1 semana y D en 2 semanas. Las Rutas Críticas ahora son: A-F ; A-D-G; B-G todas con 9 semanas según se muestra en el siguiente informe de WINQSB:

Es importante destacar que NO se puede seguir reduciendo la duración del proyecto aún cuando algunas actividades aún son factibles de apurar. Esto se justifica en general porque al menos una Ruta Crítica no se puede reducir y en dicho caso no tiene sentido destinar más recursos si esto no se verá reflejado en la duración total del proyecto. Por ejemplo, aún podemos reducir la duración de B de 5 a 4 semanas, sin embargo, la duración de la ruta A-D-G no se puede seguir reduciendo.

Importante: Recomendamos revisar el artículo Formulación y Resolución de un Modelo de Programación Lineal para reducir la duración de un Proyecto (Crashing) que detalla cómo a través de un modelo de optimización encontrar aquellas actividades que deben reducir su duración de modo de desarrollar el proyecto en el menor costo posible (dado un tiempo objetivo). En este contexto un artículo complementario es Cómo determinar la Duración Óptima de un Proyecto a través del Análisis de Crashing.

Diferencias entre la Programación No Lineal y la Programación Lineal

El supuesto de la proporcionalidad de la Programación Lineal (PL) no siempre es adecuado para representar de buena forma situaciones de naturaleza real que requieren de un modelo de optimización como apoyo para el proceso de toma de decisiones.

Cabe señalar que un modelo de Programación No Lineal (PNL) es aquel donde la función objetivo y/o las restricciones son funciones no lineales de las variables de decisión.

En este sentido la Programación No Lineal permite enfrentar una serie de aplicaciones prácticas que requieren una representación a través de funciones no lineales.

Algunos casos característicos de la Programación No Lineal son los problemas de minimización de distancia, economías o deseconomías de escala, carteras de inversión, ajuste de curva, entre otros.

En general cuando formulamos un modelo de optimización no lineal esperamos que éste sea más representativo de una situación real en comparación a un modelo lineal, sin embargo, a la vez asumimos que es probable que la complejidad de la resolución aumente. Por ello quien formule un modelo debe equilibrar la representatividad del mismo con la dificultad de la resolución.

A continuación presentaremos dos modelos de optimización que comparten las mismas restricciones (que asumiremos por simplicidad que son funciones lineales) y se diferencian por la naturaleza de la función objetivo (lineal y no lineal, respectivamente). Estos ejemplos nos ayudarán a explicar algunas diferencias entre la Programación Lineal y Programación No Lineal:

Si Resolvemos Gráficamente el modelo de Programación Lineal obtenemos la solución óptima en el vértice C (X=14/5 Y=8/5 y valor óptimo V(P)=20,8) lo cual corresponde a una Solución Básica Factible Óptima.

En efecto, una de las propiedades básicas de la Programación Lineal es que cuando un modelo admite solución, ésta se encontrará en un vértice (o tramo frontera en el caso Infinitas Soluciones Óptimas) del dominio de soluciones factibles. (Recomendación: Ver Teorema Fundamental de la Programación Lineal).

En cuanto a la resolución del modelo de Programación No Lineal, las curvas de nivel de la función objetivo no lineal tiene la forma de circunferencias concéntricas desde la coordenada (X,Y)=(2,4). Como la función objetivo es de minimización, buscamos la circunferencias de menor radio (o diámetro) que intercepte por primera vez el dominio de soluciones factibles. Esto se alcanza en (X,Y)=(1,2,2,4).

El resultado anterior se puede verificar mediante la aplicación de las condiciones de optimalidad que establece el Teorema de Karush-Kuhn-Tucker (KKT) al ser éste un problema de Programación No Lineal restringido.

Conclusión: Si un modelo de Programación No Lineal admite solución óptima, ésta se puede encontrar en cualquier punto del dominio de soluciones factibles.

Por ejemplo, si la función objetivo estuviese centrada en la coordenada (X,Y)=(2,1) ésta ya sería la solución óptima del problema. Notar que esta situación (solución en un punto interno del dominio factible) NO sería posible en la resolución de un modelo de Programación Lineal.

En los artículos de la categoría de Programación No Lineal analizamos algunos algoritmos especializados para la resolución de modelos no lineales como también herramientas computacionales para enfrentar este tipo de problemas.

Interpretación del Informe de Sensibilidad de Restricciones de Solver

Continuando con el Análisis de Sensibilidad (o Análisis Postoptimal) en la resolución de modelos de Programación Lineal, en este artículo analizaremos la interpretación del Informe de Sensibilidad (o Informe de Confidencialidad en algunas de las versiones de Office que datan del año 2010 a la fecha) de restricciones de Solver, comúnmente conocido como el análisis del Precio Sombra de cada una de las restricciones.

Por ejemplo, la versión de Solver disponible con Office 365 ofrece la siguiente interfaz para obtener el Informe de Sensibilidad (luego de alcanzar la solución óptima del problema en su escenario base).

En el caso de la versión de Solver compatible con Office 2007 y Office 2003, la interfaz es la siguiente:

De modo de ilustrar su correcta interpretación, a continuación consideraremos nuevamente nuestro ejemplo de Programación Lineal:

Con solución óptima X=14/5 Y=8/5 y valor óptimo V(P)=20,8. El Informe de Restricciones de Solver corresponde a:

Las filas del Informe de Restricciones corresponden a las restricciones 1 y 2, respectivamente.

En el caso de la restricción 1 el Precio Sombra es de 1,2 y el valor de la restricción (lado derecho) es igual a 12. Para dicho parámetro (lado derecho) se permite un aumento de de 9,33 y una disminución de 4, es decir, el lado derecho de la restricción 1 puede variar entre [8, 21,33] (12-4, 12+9,33) y el Precio Sombra de magnitud 1,2 seguirá siendo válido (es decir, se conserva la base óptima).

Esto significa que si, por ejemplo, el lado derecho de la restricción 1 aumenta en 1 unidad y el resto de los parámetros del modelo permanecen constantes, el nuevo valor óptimo será: V(P)=20,8+1*1,2=22.

Ahora bien, si por ejemplo, el lado derecho de la restricción 1 disminuye a 10 el nuevo valor óptimo será: V(P)=20,8-2*1,2=18,4.

Finalmente si la variación del lado derecho esta fuera del intervalo [8, 21,33] NO se puede utilizar el Precio Sombra para poder predecir cuál será el nuevo valor óptimo. Esto se debe a que la nueva solución óptima ya no se encontrará con las mismas restricciones activas, es decir, cambia la base óptima.

Al respecto recomendamos ver el tutorial sobre Cómo calcular gráficamente el Precio Sombra de una Restricción.

De forma análoga, para la restricción 2 el Precio Sombra es de 0,4 y este valor es válido si su lado derecho varía entre [9, 24] (16-7, 16+8). Por ejemplo, si el lado derecho de la restricción 2 aumenta en 3 unidades (y el resto de los parámetros permanece constante) el nuevo valor óptimo será: V(P)=20,8+3*0,4=22.

Cómo calcular la Probabilidad de Instock asociado al Inventario

Una supuesto frecuente de los modelos de Gestión de Inventarios sencillos es considerar que la demanda a la cual una empresa se enfrenta es conocida, es decir, no existe incertidumbre. Este supuesto da origen a Modelos Deterministas de inventarios como el de Cantidad Económica de Pedido (EOQ) con o sin Descuentos por Cantidad, Producción y Consumo Simultaneo (POQ), entre otros.

Si bien los Modelos Deterministas para la Gestión de Inventarios resultan ser útiles, en la mayor parte de las aplicaciones prácticas, es muy difícil mantener como razonable y representativo el supuesto de una demanda constante y conocida.

Para enfrentar esta situación se proponen Modelos Estocásticos, es decir, donde la demanda presenta un comportamiento aleatorio el cual puede o no ser estimado por una distribución de probabilidad conocida o en su defecto por una distribución empírica.

En este contexto de demanda aleatoria no se puede asegurar a ciencia cierta si una determinada cantidad de unidades en inventario serán suficientes para satisfacer los requerimientos de demanda de un producto. Sin embargo, si se logra perfilar el comportamiento de la demanda (aleatoria) se estará en condiciones de poder estimar que tan probable es satisfacer la demanda dada una cierto tamaño del inventario.

Uno de los indicadores de gestión que se utiliza frecuentemente es el Instock, el cual bajo un escenario de demanda con incertidumbre indica la probabilidad de satisfacer en forma íntegra la demanda (es decir, evitar quiebres de stock) para un determinado nivel de inventario.

Ejemplo del Cálculo del Instock

Para graficar este concepto consideremos que una empresa tiene 900 unidades de un producto en inventario y enfrenta una demanda por el mismo que se puede representar por una Distribución Normal con media 800 unidades ( $\mu=800$ ) y Desviación Estándar de 100 unidades ( $\sigma=100$ ). Nos interesa calcular la Probabilidad de Instock, es decir, la probabilidad que la demanda sea menor o igual a 1.000 unidades:

La Probabilidad de Instock por tanto es de un 84,13%. Para obtener la probabilidad asociada a un determinado valor de Z utilizando la Distribución Normal Estándar podemos utilizar una tabla de probabilidad que frecuentemente se incluyen como anexos en los libros de probabilidad básica o en su defecto podemos utilizar la fórmula de Excel =DISTR.NORM.ESTAND(Z). (En nuestro caso Z=1 destacado con color rojo en la tabla a continuación).

De este modo, la probabilidad de incurrir en un quiebre de stock dado un inventario de Q=900 unidades es de un 15,87% que se representa como el área achurada a la derecha de las 900 unidades.

Interpretación del Informe de Sensibilidad de Celdas Cambiantes (Solver)

Cuando Resolvemos un modelo de Programación Lineal con Solver de Excel utilizamos una estimación de los parámetros (constantes) los cuales generalmente hacen referencia a disponibilidad de recursos, precios, costos, etc. En este contexto nos interesa simular el impacto en los resultados ante variaciones marginales de dichos parámetros sin la necesidad de resolver un nuevo modelo de optimización.

Este objetivo se puede alcanzar a través de los Informes de Sensibilidad de Solver los cuales se pueden generar una vez resuelto un escenario base para un modelo de optimización lineal, seleccionando la opción “Sensibilidad” (o Confidencialidad en versiones recientes de Office) según se muestra a continuación:

El siguiente análisis explica cómo interpretar el Informe de Sensibilidad de Celdas Cambiantes de Solver para el siguiente modelo de Programación Lineal:

Con solución óptima X=14/5 Y=8/5 y valor óptimo V(P)=20,8. El Informe de Celdas Cambiantes corresponde a:

Notar que en la última columna se ha marcado con color rojo la palabra Aumento que debiese decir Disminución (este tipo de error se observa generalmente en las versiones más antiguas de Office).

El Informe de Sensibilidad de Celdas Cambiantes nos indica el intervalo de variación para cada parámetro de la función objetivo que permite mantener la actual solución óptima (asumiendo que el resto de los parámetros permanece constante).

Por ejemplo, el coeficiente que actualmente pondera a la variable X en la función objetivo de maximización es 4. El aumento permisible de 4 nos indica que el actual parámetro podría aumentar en dicha magnitud y la solución óptima actual se mantendría.

Análogamente se podría disminuir en 1 unidad (disminución permisible) y se conserva la solución actual.

En conclusión, el Intervalo de Variación para el parámetro que pondera a la variable X en la función objetivo que conserva la actual solución óptima es entre [3,8].

Siguiendo un procedimiento similar se puede demostrar que el intervalo de variación para el parámetro asociado a la variable Y en la función objetivo que conserva la actual solución óptima es entre [3,8] (sólo es una coincidencia que sean los mismos intervalos para cada parámetro).

Por ejemplo, un cambio en uno de los parámetros de la función objetivo afecta la pendiente de ésta (curvas de nivel) que en la medida que se encuentre en el intervalo de variación previamente determinado mantendrá al vértice C como solución óptima del problema.

Una forma sencilla de corroborar estos resultados es mediante el Método Gráfico en Programación Lineal. Adicionalmente en el artículo Análisis de Sensibilidad Método Gráfico se detalla el procedimiento para obtener los intervalos de variación para los parámetros tanto en la función objetivo como en las restricciones del problema. Recomendamos revisar ambos artículos de modo de favorecer la comprensión de este tipo de análisis.