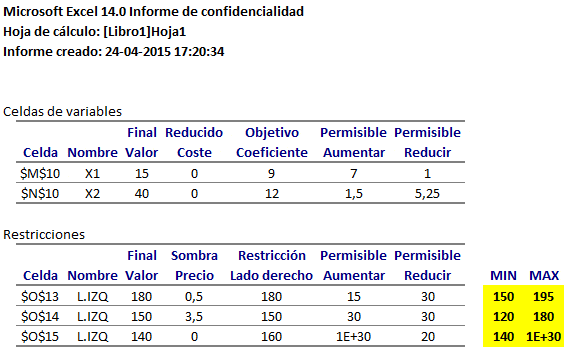
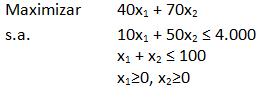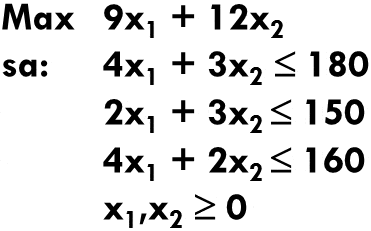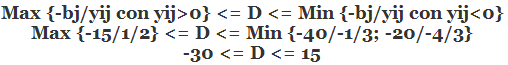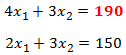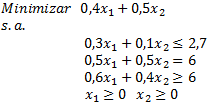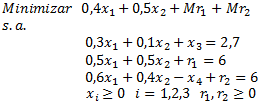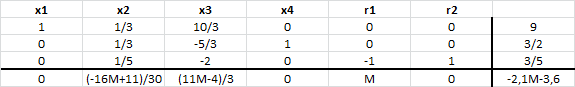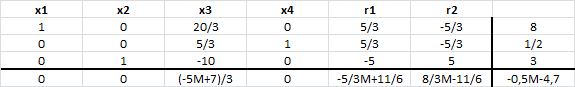resolución gráfica Archivos - Página 2 de 6

Problema de Planificación Forestal resuelto con Graphic Linear Optimizer (GLP)

El software Graphic Linear Optimizer (GLP) es una excelente herramienta que permite resolver gráficamente modelos de Programación Lineal. GLP fue desarrollado bajo la supervisión del profesor Jeffrey Moore (Ph. D) perteneciente a la Universidad de Stanford en Estados Unidos. En el siguiente artículo se muestra la utilización de Graphic LP Optimizer o GLP versión 2.6 en la resolución de un modelo de Programación Lineal en 2 variables que aborda una problemática de planificación forestal.

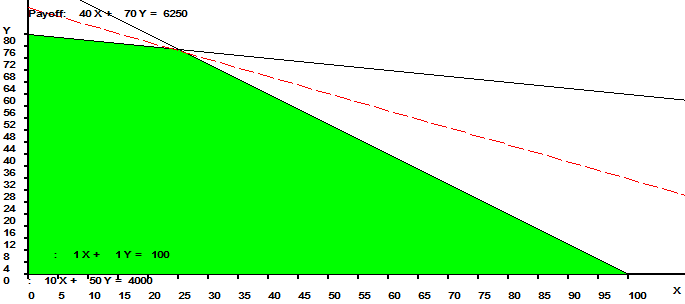
Una compañía forestal tiene un predio de 100 hectáreas de bosques para explotar. Talar y dejar el suelo para uso agrícola tiene un costo inmediato de M$10 por hectárea y un retorno posterior de M$50 por hectárea. Una alternativa es talar y plantar pino que tiene un costo inmediato de M$50 por hectárea y un retorno posterior de M$120 por hectárea. De aquí que los beneficios netos de ambos planes sean de M$40 y M$70 por hectárea, respectivamente. Desafortunadamente, el segundo plan no puede ser aplicado a todo el terreno ya que sólo se dispone de recursos inmediatos por M$4000. Formule y resuelva gráficamente utilizando el software Graphic Linear Optimizer (GLP) un modelo de Programación Lineal que provea el plan más eficiente de explotación, indicando claramente la solución óptima y valor óptimo.

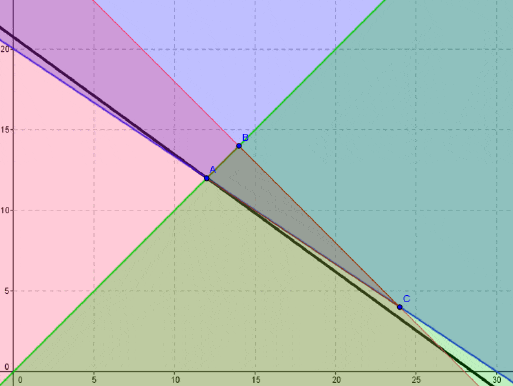
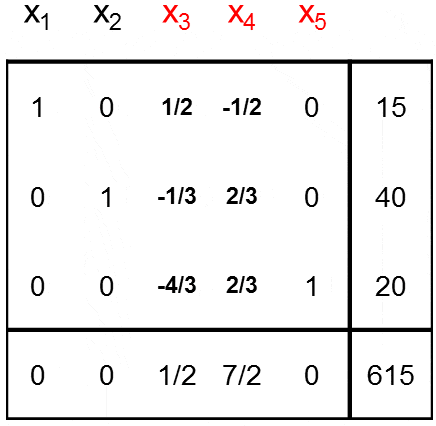
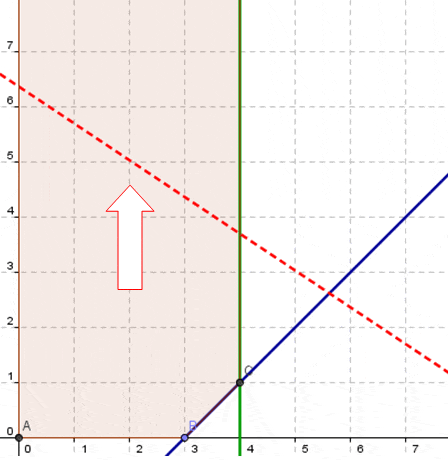
El modelo de Programación Lineal para la situación anterior es:

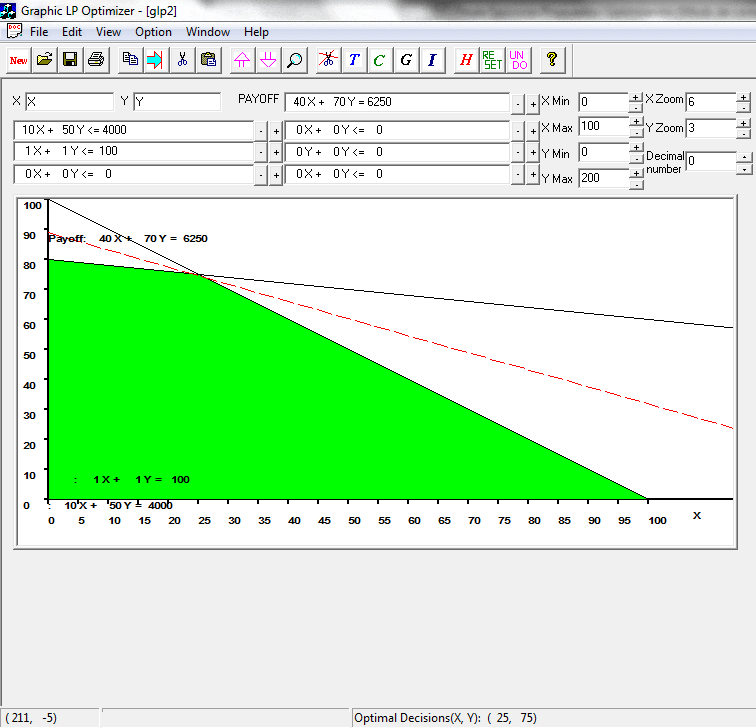
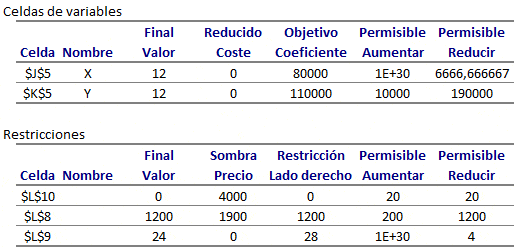
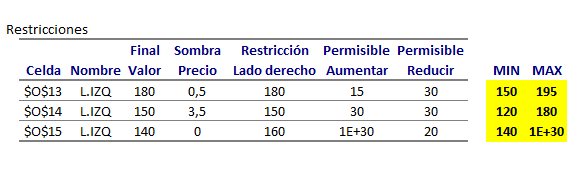
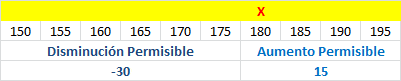
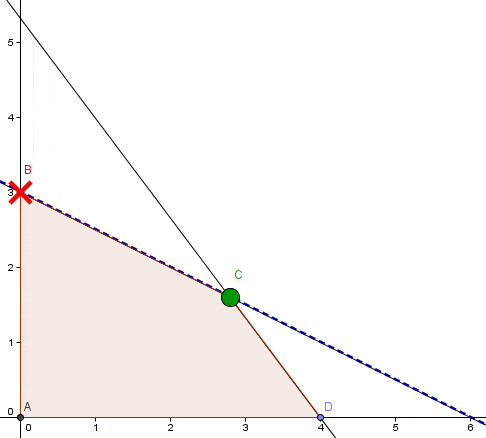
Donde $x_{1}$ representa las hectáreas para talar y dejar para uso agrícola y $x_{2}$ las hectáreas para talar y plantar pino. En la siguiente imagen se muestra un extracto de la interfaz del programa GLP donde al pie de la misma se observa la solución óptima del problema con $x_{1}=25$ y $x_{2}=75$ . El valor óptimo es 6.250 el cual se encuentra en la fila con la etiqueta PAYOFF.

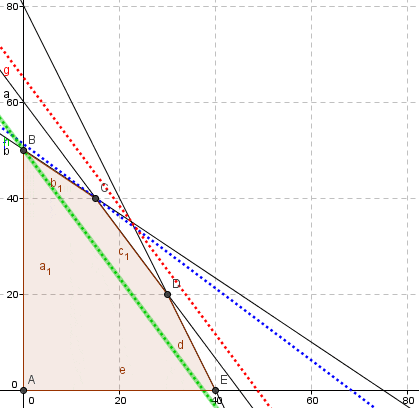
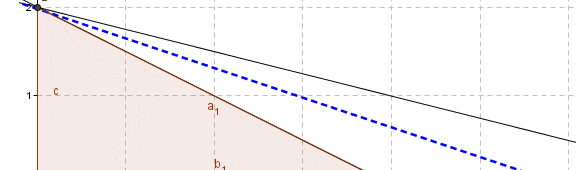
El software GLP permite ajustar tanto la escala del gráfico como un zoom personalizado en cualquiera de los ejes de coordenadas. No obstante recomendamos hacer uso de la funcionalidad Auto Zoom que ajusta automáticamente la representación gráfica a una escala adecuada en relación a la magnitud de los datos de origen.

A continuación dejamos a nuestros usuarios un enlace de descarga del software Graphic Linear Optimizer o GLP para que puedan probar sus distintas funcionalidades.

[sociallocker]

MUCHAS GRACIAS!. DESCARGA AQUÍ EL ARCHIVO

[/sociallocker]

Problema de Arriendo de Buses para Transporte de Pasajeros en Programación Lineal

El siguiente problema de Programación Lineal consiste en determinar una política óptima de arriendo de buses para el transporte de pasajeros que minimice los costos asociados a su arriendo y satisfaga los requerimientos de transporte y otras condiciones adicionales que se deseen imponer.

El Centro de Alumnos de Ingeniería Industrial de una respetada universidad desea celebrar el día del alumno en la playa. Este paseo está planificado para 1.200 alumnos como mínimo. Una empresa de transporte ofrece 2 tipos de buses pero solo cuenta con 28 conductores. La tabla de abajo indica la capacidad y el costo de arriendo de cada tipo de bus:

Para mantener el equilibrio de su flota, la empresa de transporte impone la condición de que el número de buses tipo B arrendados no puede exceder el número de buses tipo A arrendados. Formule y resuelva un modelo de Programación Lineal que permita determinar cuántos buses de cada tipo hay que arrendar para el paseo de modo que resulte lo más económico para el Centro de Alumnos.

Variables de Decisión:

$x$ : Cantidad de Buses Tipo A arrendados
$y$ : Cantidad de Buses Tipo B arrendados

Función Objetivo:

Minimizar $80.000x+110.000y$

Restricciones:

Cantidad de Alumnos: $40x+60y\geq 1.200$
Cantidad de Conductores: $x+y\leq 28$
Condición de Flota: $x-y\geq 0$
No Negatividad: $x,y\geq 0$

El dominio de soluciones factibles del problema esta dado por el polígono ABC según se detalla a continuación (representación gráfica realizada con el software Geogebra). En particular la solución óptima corresponde al vértice A donde $x=12$ e $y=12$ , con valor óptimo $V(P)=80.000*12+110.000*12=2.280.000$ .

Notar que si bien el problema fue modelado como uno de Programación Lineal, dadas las características del problema sería deseable obtener una solución entera para las variables de decisión (dado que no es posible arrendar una fracción de buses y asumir por ejemplo que el costo del mismo es proporcional a la capacidad ocupada). No obstante en el ejemplo propuesto la solución óptima obtenida cumple de forma natural con las condiciones de integralidad, lo que indica que sus resultados son idénticos al problema de Programación Entera asociado (es decir, aquel al cual se le agregan de forma explícita las condiciones de enteros para las variables de decisión).

De forma complementaria al análisis anterior se pueden responder las siguientes preguntas correspondientes al análisis de sensibilidad o postoptimal:

1. Determine cuánto podría variar el costo de arriendo del Bus tipo A que conserve la solución óptima. Si C1 (costo arriendo del Bus tipo A) varía en el intervalo entre [73.333,3 , ∞[ se conserva la actual solución óptima.

2. Determine el impacto en el valor óptimo del problema si se elimina la condición que el número de buses tipo B arrendados no puede exceder el número de buses tipo A arrendados. El precio sombra de la restricción de condición de flota es 4.000. Luego si se elimina la condición de flota la solución óptima se alcanza en la mínima variación $(x,y)=(0,20)$ para una reducción permisible del lado derecho de dicha restricción en 20 unidades. Luego el nuevo valor óptimo es $V(P)=2.280.000+(-20-0)*4.000=2.200.000$ .

Cálculo del Intervalo de Variación del Lado Derecho que conserva la Base Óptima

Una vez concluidas las iteraciones del Método Simplex y en el caso de alcanzar una solución básica factible óptima, puede resultar de interés determinar un intervalo de variación para un parámetro del vector de los lados derechos de las restricciones que permita conservar la geometría del problema. Esto implica que se conservan las restricciones activas originales en el nuevo escenario (es decir, se mantiene la base óptima) que se genera a partir de la modificación (individual) de un parámetro o coeficiente del lado derecho. Para ilustrar el resultado anterior consideremos el siguiente modelo de Programación Lineal.

Luego de llevar a la forma estándar el modelo anterior agregando $x_{3}$ , $x_{4}$ y $x_{5}$ como las variables de holgura de las restricciones 1, 2 y 3, respectivamente, y aplicar las iteraciones necesarias del Método Simplex, se alcanza la siguiente tabla final (óptima):

La solución óptima es $x_{1}=15$ y $x_{2}=40$ con valor óptimo $V(P)=615$ . El valor de las variables de holgura en el óptimo $x_{3}$ , $x_{4}$ y $x_{5}$ es 0, 0 y 20, respectivamente. Luego se puede concluir que la solución óptima del problema se alcanza con las restricciones 1 y 2 activas (notar que sus respectivas holguras con variables no básicas en el óptimo) y la base actual esta conformada por las variables $x_{1}$ , $x_{2}$ y $x_{5}$ .

Sabemos adicionalmente que, por ejemplo, el costo reducido de la variable de holgura $x_{3}$ representa el precio sombra asociado a la primera restricción ( $\pi_{1}=1/2$ ). No obstante desconocemos en qué intervalo puede variar el parámetro del lado derecho de la restricción 1 (actualmente $b_{1}=180$ ) de modo que se conserve la base óptima y por tanto nos permita hacer un correcto uso de la información del precio sombra.

Para ello se propone la siguiente fórmula que permite encontrar el intervalo de variación para un lado derecho que conserva la base óptima:

Max {-bj/yij con yij>0} <= D <= Min {-bj/yij con yij<0}

Por ejemplo determinemos el intervalo para el parámetro $b_{1}$ :

En consecuencia $b_{1}$ puede disminuir en 30 unidades y aumentar en 15 unidades y se conserva la base óptima. Es decir, si $b_{1}\epsilon [150,195]$ se mantiene la base óptima.

El resultado anterior se puede corroborar gráficamente. La solución óptima se encuentra en el vértice C donde las restricciones 1 y 2 son activas (notar la curva de nivel que pasa por el vértice óptimo es la línea punteada de color azul). Si para el lado derecho de la restricción 1 consideramos $b_{1}=150$ se obtiene la línea de color verde y para $b_{1}=195$ la línea de color rojo. En estos casos si bien se modifica el dominio de soluciones factibles, la solución óptima conserva las actuales restricciones activas (y por ende cuando $b_{1}$ adopta un valor fuera de este intervalo cambia la geometría del problema o base óptima).

Esto es consistente con el Informe de Confidencialidad de Solver. En particular el reporte de restricciones donde se aprecia el aumento y reducción permisible que conserva la actual base óptima:

Por ejemplo, ¿cuál es el nuevo valor óptimo si el lado derecho de la restricción 1 ahora es $b_{1}=190$ ?. Como $b_{1}=190\epsilon[150,195]$ , entonces $V(P)=615+\Delta b_{1}\pi _{1}=615+(190-180)*(1/2)=620$ . ¿Cuál es la nueva solución óptima?. Como sabemos que se conservan las restricciones activas en el óptimo para la variación propuesta, la solución óptima del nuevo escenario se obtiene simplemente resolviendo el siguiente sistema de ecuaciones (notar que la restricción 1 y 2 se conservan activas):

De donde $x_{1}=20$ y $x_{2}=110/3$ , que al evaluar en la función objetivo se obtiene: $V(P)=9*(20)+12*(110/3)=620$ corroborando el resultado anterior. Dejamos al lector el desafío de aplicar los conceptos presentados en este articulo para encontrar un intervalo para $b_{2}$ y $b_{3}$ que conserve la base óptima.

Casos Especiales en la Programación Lineal detectados con el Método Simplex

En la resolución de un modelo de Programación Lineal se pueden enfrentar ciertos casos especiales que merecen particular atención. Estos casos (infinitas soluciones óptimas, problema no acotado sin solución óptima, problema infactible, solución óptima degenerada) se pueden detectar a través de la aplicación del Método Simplex según hemos tratado previamente en el Blog. A continuación un resumen de dichos escenarios:

Infinitas Soluciones Óptimas: Se detecta cuando luego de alcanzar una solución básica factible óptima, al menos una variable no básica tiene costo reducido igual a cero. La siguiente imagen representa esta situación donde la solución óptima (infinitas) se alcanza en el tramo entre los vértices B y C. En efecto se puede representar de forma general las soluciones óptimas como: $(x,y)=\lambda (0,3)+(1-\lambda )(2,2)$ con $0\leq \lambda\leq 1$ .

Problema No Acotado: En las iteraciones del Método Simplex un problema no acotado se detecta cuando al calcular el criterio de factibilidad o mínimo cuociente que determina la variable que deja la base, todas las entradas en la columna de la variable no básica entrante son negativas o cero, por tanto no existe denominador válido (mayor a cero) que permita determinar el pivote. En la siguiente representación gráfica se puede apreciar que las curvas de nivel de la función objetivo crecen en la dirección del vector gradiente, donde en particular el dominio de soluciones factibles es no acotado para los valores que puede adoptar la variable $x_{2}$ .

Es importante destacar que el hecho que un dominio de soluciones factibles sea no acotado no implica necesariamente que el problema de Programación Lineal no tiene solución.

Problema Infactible: Si al finalizar la Fase I del Método Simplex de 2 Fases el valor de la función objetivo es distinto a cero, entonces el problema lineal es infactible, es decir, el dominio de soluciones factibles es vacío al existir restricciones incompatibles (por ejemplo en el gráfico a continuación el área azul no se intersecta con el área color rojo).

Solución Óptima Degenerada: Cuando se presenta un empate el el cálculo de la condición de factibilidad del Método Simplex, al menos una variable básica será cero en la siguiente iteración, caso en el cual se dice que la nueva solución es degenerada. Esto implica que el modelo tiene al menos una restricción redundante.

Método de la M Grande (o Gran M) en Programación Lineal

En el contexto de la aplicación del Método Simplex no siempre es inmediata la obtención de una solución básica factible inicial, en las variables originales del modelo. Para conseguir esto existen varios procedimientos como son el Método Simplex de 2 Fases y el Método de la M Grande (o Gran M) el cual abordaremos en este artículo. Para ello consideremos el siguiente modelo de Programación Lineal en 2 variables:

A continuación agregamos las variables no negativas $x_{3}$ (holgura restricción 1), $r_{1}$ (auxiliar restricción 2), $x_{4}$ (exceso restricción 3) y $r_{2}$ (auxiliar restricción 3). El modelo ahora es:

Donde el parámetro M es una constante positiva suficientemente grande para representar una penalización adecuada en la función objetivo. La tabla inicial del método esta dada por:

Antes de continuar con las iteraciones se debe procurar que el costo reducido de las variables $r_{1}$ y $r_{2}$ sean ceros. Para ello multiplicamos por -M la fila 2 y la fila 3 y luego sumamos a la fila 4, obteniendo lo siguiente:

Ahora debemos seleccionar que variable no básica ingresa a la base. El menor costo reducido corresponde a la variable $x_{1}$ en consecuencia dicha variable ingresa a la base. Luego calculamos el mínimo cuociente en dicha columna: $Min \begin{Bmatrix}{\frac{27/10}{3/10}, \frac{6}{1/2}, \frac{6}{3/5}}\end{Bmatrix}=9$ , el cual se alcanza en la fila 1, por tanto la variable $x_{3}$ deja la base. Se actualiza la tabla:

Siguiendo con las iteraciones ahora la variable $x_{2}$ entra a la base. El criterio de factibilidad indica que: $Min \begin{Bmatrix}{\frac{9}{1/3}, \frac{3/2}{1/3}, \frac{3/5}{1/5}}\end{Bmatrix}=3$ la variable $r_{2}$ abandona la base (el pivote se encuentra en la fila 3). Actualizamos la tabla:

Una nueva iteración indica que $x_{3}$ ingresa a la base. El mínimo cuociente en la respectiva columna es: $Min \begin{Bmatrix}{\frac{8}{20/3}, \frac{1/2}{5/3}}\end{Bmatrix}=3/10$ (recordar que se omiten denominadores menores a cero). Ahora el pivote se encuentra en la fila 2 y en consecuencia $x_{4}$ deja la base. Se actualiza la tabla:

Se ha alcanzado la solución óptima con $x_{1}=15/2$ y $x_{2}=9/2$ . Notar que las variables auxiliares (r1 y r2) son no básicas en el óptimo. El valor óptimo es 21/4 (notar que el signo esta cambiado).

Para una mejor comprensión de los resultados alcanzados a continuación se presenta la resolución gráfica del problema haciendo uso del software Geogebra. El dominio de soluciones factibles corresponde a la recta que une los vértices A y B. Adicionalmente se muestra la curva de nivel que pasa por la solución óptima (vértice B).

Teóricamente se espera que en la aplicación del Método de la M Grande las variables auxiliares sean no básicas en el óptimo. Si el modelo de Programación Lineal es infactible (es decir, si las restricciones no son consistentes), la iteración del Método Simplex final incluirá al menos una variable artificial como básica.

Adicionalmente la aplicación de la técnica de la M Grande implica teóricamente que M tiende a infinito. Sin embargo al usar la computadora M debe ser finito, pero suficientemente grande. En específico M debe ser lo bastante grande como para funcionar como penalización, al mismo tiempo no debe ser tan grande como para perjudicar la exactitud de los cálculos del Método Simplex, al manipular una mezcla de números muy grandes y muy pequeños.