En el siguiente artículo detallaremos cómo funciona el Método Simplex a través de un ejemplo sencillo correspondiente a un modelo de Programación Lineal que considera 3 variables de decisión.
El Método Simplex corresponde a un algoritmo iterativo publicado por George Bernard Dantzig en el año 1947 en donde se busca alcanzar el máximo (o mínimo) de una función lineal compuesta por un conjunto de variables que deben satisfacer condiciones impuestas por restricciones lineales en forma de inecuaciones.
En este contexto, el objetivo de este artículo es definir en detalle distintas aproximaciones para la resolución de un modelo de Programación Lineal utilizando el Método Simplex, además de discutir sobre sus principales características.
Con tal propósito en perspectiva consideremos el siguiente modelo de optimización lineal:
Ejemplo del Método Simplex (Utilizando Diccionarios)
Un paso preliminar consiste en incorporar las denominadas variables de holgura. De modo de comprender este concepto consideremos la primera restricción:
Para cada solución factible , el valor del lado izquierdo será a lo más el valor del lado derecho; o eventualmente existirá una diferencia (holgura) entre estos 2 valores.
De esta forma definimos como variable de holgura de dicha restricción, la cual se puede denotar por
, donde
. De forma análoga se pueden definir las variables de holgura (no negativas)
y
para las restricciones 2 y 3, respectivamente. Finalmente podemos describir la función objetivo
utilizando
de forma compacta.
En resumen, para cada selección de valores de las variables y
podemos definir valores para las variables
, y
utilizando las siguientes fórmulas (conocido comúnmente como diccionarios según la terminología utilizada en el libro Linear Programming de Vasek Chvátal):
El objetivo del Método Simplex es lograr sucesivas mejoras para el valor de la función objetivo asociada a la selección de alguna solución factible. Repetir dicho procedimiento un numero finito de veces debería permitir eventualmente alcanzar la solución óptima del problema lineal en estudio.
Para inicializar el Método Simplex necesitamos una solución factible. En nuestro ejemplo esto es sencillo y se puede alcanzar simplemente fijando las variables en cero. De esta forma se alcanzan los siguientes resultados:
En el contexto del objetivo planteado anteriormente, debemos buscar una solución factible que permita alcanzar un mayor valor para . Si, por ejemplo, mantenemos
e incrementamos el valor de
obtenemos
, de modo que si
se obtiene
(y
). Mejor aún, si
(manteniendo
), se obtiene
(y
).
Sin embargo, si asumimos (conservando
) el valor de la función objetivo ahora es
, pero
que claramente no satisface las condiciones de no negatividad para las variables.
Por tanto la pregunta relevante es: ¿cuánto se puede incrementar el valor de
(manteniendo
al mismo tiempo) y seguir conservando la factibilidad (
)?.
La condición implica
; de forma similar
implica
y
implica
. Claramente de estas 3 cotas para la variable
la más restrictiva es
, de modo que incrementamos el valor de
hasta ese valor de modo de obtener una nueva solución:
Que claramente constituye una mejora para el valor de la función objetivo en comparación al valor inicial .
A continuación debemos buscar una nueva solución factible que sea aún mejor que la que acabamos de encontrar. Para ello la variable que cambió su valor desde cero a un número positivo (12,5), debe cambiar su lugar desde el lado derecho al lado izquierdo del sistema de ecuaciones. De forma análoga, la variable
que cambio su valor de un número positivo a cero debe cambiar de lugar desde el lado derecho al lado izquierdo.
De esta forma y luego de cierta manipulación algebraica podemos reescribir en términos de
según se observa a continuación:
Luego, con el objetivo de expresar y
en términos de
, simplemente substituimos el resultado anterior en las filas correspondientes:
De esta forma nuestro sistema de ecuaciones (diccionario) queda definido por:
Como lo hicimos en la primera iteración debemos intentar incrementar el valor de la función objetivo () seleccionando una variable adecuada en el lado derecho, mientras que al mismo tiempo mantenemos las restantes variables del lado derecho en cero. En este sentido se puede observar que aumentar el valor de las variables
o
generaría una disminución en el valor de
que va en sentido contrario a nuestro objetivo de maximizar el valor de la función objetivo.
Por tanto, la única selección de una variable en el lado derecho que permitirá aumentar el valor de
es seleccionar la variable
.
¿Cuánto debemos incrementar el valor de ?. La respuesta se puede obtener directamente del sistema de ecuaciones anterior, considerando
, la restricción
implica que
; la restricción
no impone condiciones adicionales y la restricción
implica
. En consecuencia
es el mejor valor que puede adoptar dicha variable.
La nueva solución corresponde a:
El valor de paso de 12,5 a 13 al cabo de una iteración del Método Simplex.
A continuación actualizamos el sistema de ecuaciones donde las variables que adoptan valores positivos se encontraran en el lado izquierdo, mientras las variables igual a cero estarán en el lado derecho. De este modo pasamos la variable
al lado izquierdo, donde
que permite substituir en el resto de las ecuaciones:
Notar que no es posible seguir aumentando el valor de la función objetivo mediante un incremento de las variables del lado derecho
(en efecto, el valor de
decrecería). En consecuencia estamos en presencia de la solución óptima del problema:
con valor óptimo
.
El procedimiento anterior basado en diccionarios favorece una mejor comprensión conceptual de los fundamentos sobre los que se basa el Método Simplex. De forma complementaria a continuación presentaremos a modo de contraste las iteraciones del Método Simplex utilizando tablas (o tableau) que comúnmente corresponde a la forma en la cual se presenta el algoritmo en cursos de pregrado.
Ejemplo del Método Simplex (Utilizando Tableau)
Consideremos nuevamente nuestro problema de Programación Lineal:
A continuación incorporamos las variables de holgura (no negativas) que por definición tienen coeficiente nulo (cero) en la función objetivo. De esta forma obtenemos la forma estándar (*):
(*). Para nuestros efectos consideraremos que la forma estándar de un modelo de Programación Lineal esta dada por
, siendo este formato el que preferentemente hemos utilizado para desarrollar las iteraciones del Método Simplex en otros artículos relacionados en nuestro sitio. En consecuencia la selección de dicho formato es meramente convencional.
Retomando nuestro ejemplo, el tableau inicial queda definido por:
Las variables de holgura definen una Solución Básica Factible Inicial, con (las variables no básicas inicialmente corresponden a las variables originales del modelo, es decir,
que por definición adoptan un valor igual a cero.
¿Cómo verificar que el tableau inicial representa una solución básica factible óptima para el problema?.
Criterio de Optimalidad: Si en una iteración del Método Simplex se dispone de una solución básica factible y adicionalmente todos los costos reducidos son mayores o iguales que cero, parar ya que la actual solución básica factible es óptima.
En el ejemplo propuesto si bien nos encontramos frente a una solución básica factible el costo reducido de las variables no básicas son negativos, por tanto no se cumple el criterio de optimalidad, es decir, se puede seguir mejorando el valor de la función objetivo.
En este sentido consideraremos arbitrariamente como la variable que ingresa a la base, aun cuando no hay certeza que la selección de la variable no básica con el costo reducido más negativo contribuya necesariamente a la Rapidez de Convergencia del Método Simplex.
La variable que deja la base para dar lugar a se obtiene del criterio de factibilidad:
Criterio de Factibilidad: Para decidir que variable básica deja la base, es necesario calcular el mayor valor que puede tomar la variable no básica que entra a la base que garantice la factibilidad de la nueva solución básica. Para ello se considera un cuociente entre el valor de la solución básica factible actual y los coeficientes mayores a cero en la columna de la variable entrante. Si todos los cuocientes son negativos el Problema es No Acotado y por tanto no existe solución óptima.
En el ejemplo el criterio de factibilidad para la presente iteración esta dado por:
El menor cuociente se alcanza en la primera fila (restricción) que determina la variable que debe abandonar la base, en este caso, la variable . Luego se actualiza la tabla realizando operaciones filas considerando el denominador del mínimo cuociente como pivote. El objetivo es alcanzar en la columna de la variable
lo que actualmente disponemos en la columna de la variable
.
Por ejemplo, podemos dividir la fila 1 por 2 de modo de obtener un 1 en la posición del pivote. Luego sobre esta nueva fila 1 podemos multiplicarla por -4 y sumarla a la fila 2. También se puede alcanzar un cero para la variable
en la fila 3 multiplicando por -3 la nueva fila 1 y sumándola a la fila 3. Finalmente para lograr un cero en el costo reducido de
se multiplica por 5 la nueva fila 1 y se suma a la fila 4.
De este modo el tableau del Método Simplex al cabo de una iteración queda de la siguiente forma:
La solución básica factible actual corresponde a:
con valor en la función objetivo
. Se puede apreciar que dicho resultado es consistente con el enfoque de diccionarios utilizado inicialmente.
Claramente no se satisface el criterio de optimalidad dado que la variable no básica tiene costo reducido negativo. Por ello
ingresa a la base y por tanto debemos calcular nuevamente el criterio de factibilidad para determinar la variable que deberá dejar la base:
El pivote ahora se encuentra en la fila 3 y en consecuencia la variable básica debe dejar la base. Notar que no se ha considerado para el cálculo del criterio de factibilidad el coeficiente de la variable
correspondiente a la fila 2 del tableau anterior (cuyo valor es cero y por tanto el cuociente se indefine).
Actualizamos el tableau del Método Simplex obteniendo los siguientes resultados:
Los valores que adoptan las variables básicas correspondientes a esta nueva iteración es que además representa la solución óptima del modelo de Programación Lineal (dado el cumplimiento del criterio de optimalidad). Luego el valor óptimo corresponde a
.
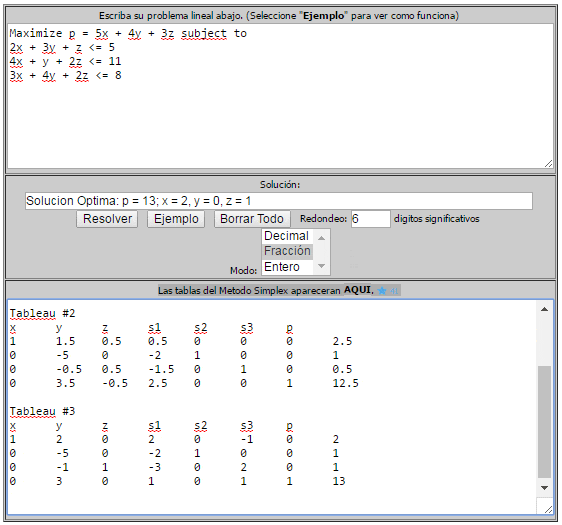
Importante: Existen herramientas computacionales y aplicaciones que permiten resolver online un problema de Programación Lineal mediante el Método Simplex. A continuación se presenta un extracto de los resultados alcanzados para nuestro ejemplo utilizando la aplicación disponible en http://www.programacionlineal.net/simplex.html.
Método Simplex (Conclusiones)
El ejemplo que hemos desarrollado en este artículo busca presentar de forma sencilla y didáctica los principales fundamentos asociados al Método Simplex. Cabe destacar que ha sido necesario para la aplicación del algoritmo llevar el modelo original a su forma estándar que como se discutió anteriormente puede tener distintas representaciones según la bibliografía que se consulte.
En este contexto, cada problema de Programación Lineal en su forma estándar cumple con las siguientes propiedades establecidas en el Teorema Fundamental de la Programación Lineal:
- Si el problema no tiene solución óptima entonces es no-acotado o infactible.
- Si tiene una solución factible, tiene una solución básica factible.
- Si el problema tiene solución óptima, tiene una solución básica factible óptima.
Cabe destacar que no siempre se dispone de una solución básica factible en las variables originales del modelo (luego de llevar el problema a su forma estándar). Si bien existen diversas estrategias algorítmicas para enfrentar esta dificultad, se propone al lector revisar los tutoriales que hemos desarrollado sobre esta problemática, en particular respecto al Método Simplex de 2 Fases, Método de la M Grande y Método Simplex Dual.
Adicionalmente con el objetivo de resumir algunas ideas principales del algoritmo hemos preparado una infografía que hemos llamado 10 Cosas que Necesitas saber sobre el Método Simplex.
Finalmente quisiéramos recordar a nuestros usuarios que en el Blog de Gestión de Operaciones se pueden encontrar a la fecha más de 80 publicaciones relativas a la Programación Lineal y la Investigación de Operaciones. De modo de favorecer una rápida búsqueda ingresa al menú Cómo Comenzar. Por último agradeceríamos compartir y difundir este material en la medida que haya sido considerado útil y evaluar este tutorial utilizando las estrellas al final de esta publicación.
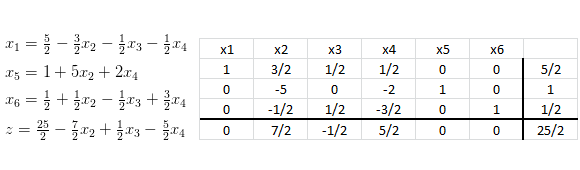
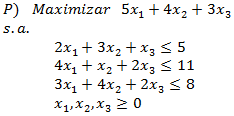
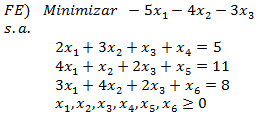
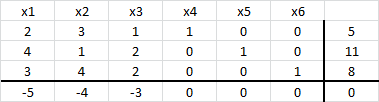
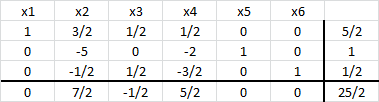
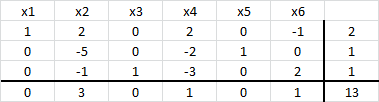
Excelente explicación, muy claro y de invaluable ayuda. Mil gracias.
Hola, muy buena la información, gracias por compartirla. Tengo una duda ingenieros, he buscado pero no encuentro respuesta alguna. Cuando una restricción tiene como termino independiente el valor de 0, en el caso de maximización y debe ser mayor o igual, ¿Qué debo hacer en ese caso?, ¿Lo multiplico por -1 o lo dejo así?
Ejemplo: 2X – 3Z >= 0
La duda me surgió por un problema que ya se que no tiene solución pero que en un programa para verificar el ejercicio me apareció que debía multiplicarlo por -1. En otros libros y páginas solo dice que se multiplica por -1 cuando es menor a 0, no igual. ¿Qué debo hacer realmente?. Gracias de antemano por su colaboración.
@David. En rigor multiplicar por -1 una restricción no tiene efectos en la definición del conjunto de soluciones factibles de un modelo de optimización y sólo podría ser requerido para llevar el modelo a una estructura deseada que, por ejemplo, facilite su implementación computacional en una determinada herramienta. Por ejemplo, si la restricción que propones fuese 2X-3Z>=-2 al multiplicar ésta por -1 quedaría -2X+3Z<=2 y que siguiendo la estructura que hemos detallado en este artículo sólo requeriría de una variable de holgura para llevar transforma ésta en una ecuación.
Doy gracias por la aportación de este tutorial, me ha ayudado mucho debido que hacia 39 años que no aplicaba nada de estos conocimientos en la construcción,gracias