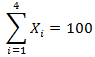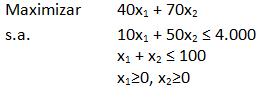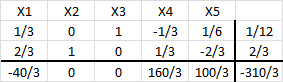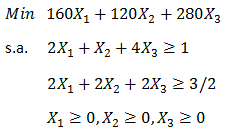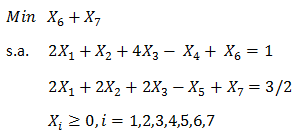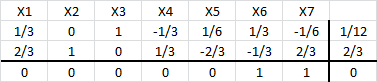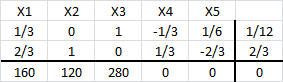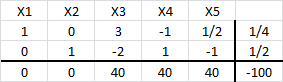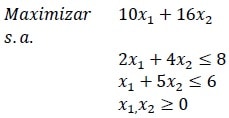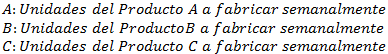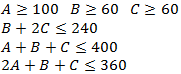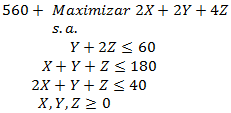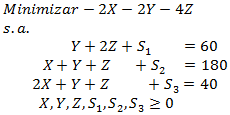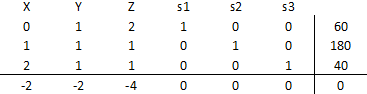Programación Lineal Archivos - Página 4 de 17

Formulación de un Problema de Aleaciones de Metales resuelto con Solver de Excel

Los modelos de Programación Lineal constituyen una excelente herramienta para representar Problemas de Mezcla de Productos en los cuales se asume que la calidad de la mezcla final en términos de los atributos propios de sus componentes, será proporcional a la participación de los insumos. En este contexto, el siguiente problema representa la situación de una empresa metalúrgica que debe determinar la combinación óptima de distintas aleaciones de metales que le permita configurar una nueva aleación a un costo mínimo. Por cierto se asume que el supuesto básico de la Programación Lineal asociado a la proporcionalidad es admisible.

Problema de Aleaciones de Metales

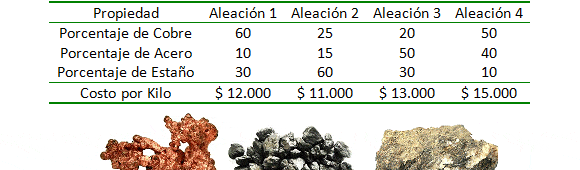
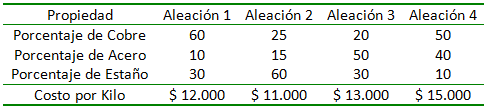
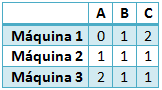
Una empresa metalúrgica desea fabricar 100 kilos de una nueva aleación que contenga no más de un 45% de Cobre, no menos de un 30% de Acero y un 20% de Estaño a partir de cuatro aleaciones que tienen las siguientes propiedades:

Formule y resuelva un modelo de Programación Lineal que permita determinar el porcentaje de cada una de las aleaciones debe contener la nueva aleación, de forma que resulte a un mínimo costo.

Variables de Decisión: Se propone definir la cantidad de kilogramos que representará cada una de las 4 aleaciones originales en la nueva aleación. Análogamente se puede definir como variables de decisión el porcentaje que representa cada aleación (original) respecto a la nueva aleación.

Función Objetivo: Se desea minimizar el costo asociado a la utilización de las distintas utilizaciones.

Restricciones: El valor que adopten las variables de decisión previamente definidas deben satisfacer las condiciones que establecen las siguientes restricciones.

Kilogramos a Producir de la Nueva Aleación: Se deben producir 100 kilogramos de la nueva aleación.

Máximo Porcentaje de Cobre: La nueva aleación debe contener como máximo un 45% de cobre.

Mínimo Porcentaje de Acero: La nueva aleación debe contenemos como mínimo un 30% de acero.

Porcentaje de Estaño: La nueva aleación debe tener exactamente un 20% de estaño.

No Negatividad: Naturalmente las variables de decisión deben adoptar valores mayores o iguales a cero.

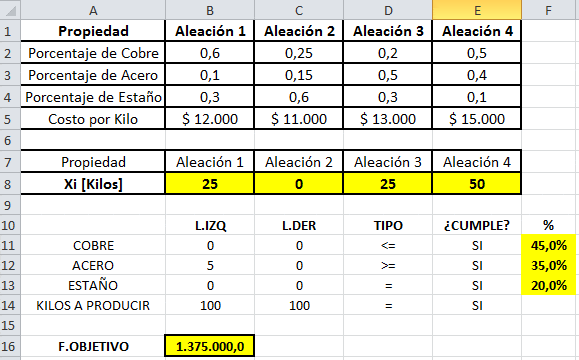
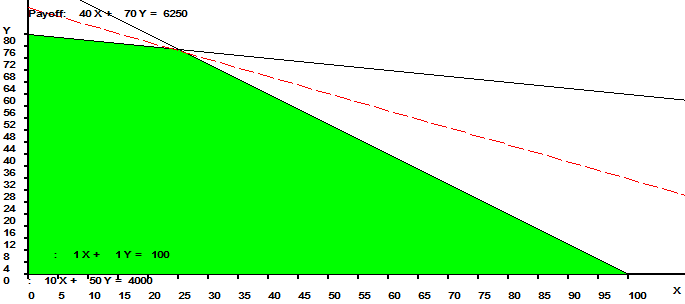
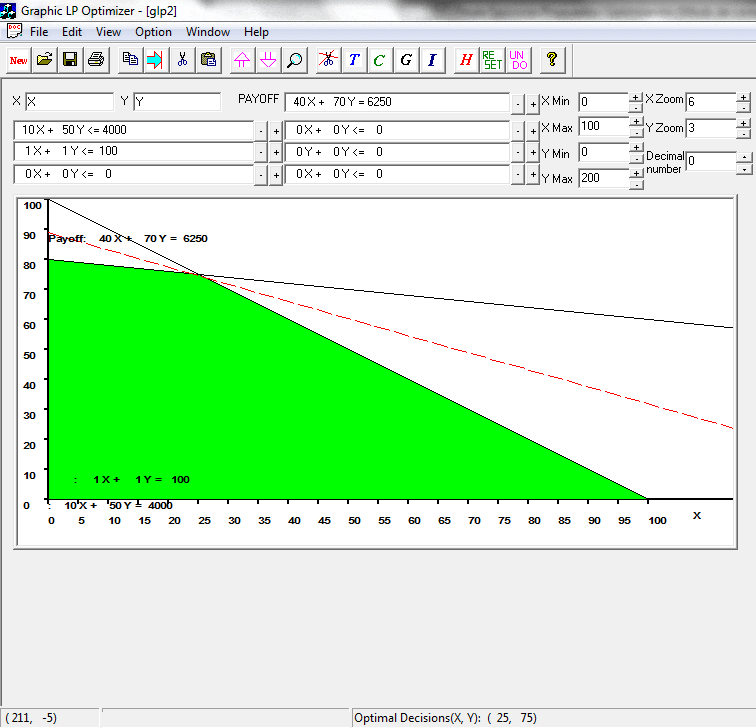
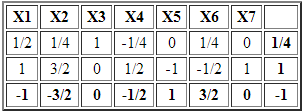
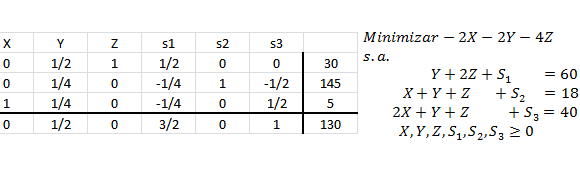
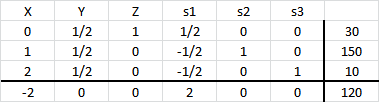
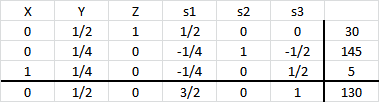
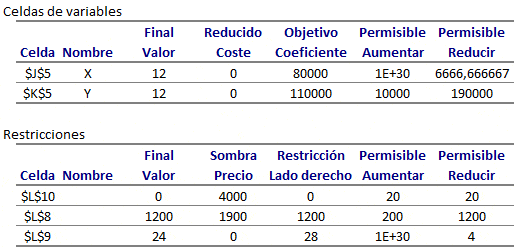
A continuación se muestra un extracto de los resultados computacionales luego de hacer uso de Solver de Excel.

La solución óptima consiste en $X_{1}=25, X_{2}=0, X_{3}=25, X_{4}=50$ , con valor óptimo $V(P)=1.375.000$ . Dicha solución representa 100 kilogramos de la nueva aleación (que en efecto corresponde a la sumatoria de la cantidad de kilos que representa cada variable) donde la nueva aleación tiene un 45% de cobre, un 35% de acero y un 20% de estaño.

¿Quieres tener el archivo Excel con la resolución en Solver del Problema de Aleaciones de Metales presentado en este artículo?

[sociallocker]

MUCHAS GRACIAS!. DESCARGA AQUÍ EL ARCHIVO

[/sociallocker]

Problema de Planificación Forestal resuelto con Graphic Linear Optimizer (GLP)

El software Graphic Linear Optimizer (GLP) es una excelente herramienta que permite resolver gráficamente modelos de Programación Lineal. GLP fue desarrollado bajo la supervisión del profesor Jeffrey Moore (Ph. D) perteneciente a la Universidad de Stanford en Estados Unidos. En el siguiente artículo se muestra la utilización de Graphic LP Optimizer o GLP versión 2.6 en la resolución de un modelo de Programación Lineal en 2 variables que aborda una problemática de planificación forestal.

Una compañía forestal tiene un predio de 100 hectáreas de bosques para explotar. Talar y dejar el suelo para uso agrícola tiene un costo inmediato de M$10 por hectárea y un retorno posterior de M$50 por hectárea. Una alternativa es talar y plantar pino que tiene un costo inmediato de M$50 por hectárea y un retorno posterior de M$120 por hectárea. De aquí que los beneficios netos de ambos planes sean de M$40 y M$70 por hectárea, respectivamente. Desafortunadamente, el segundo plan no puede ser aplicado a todo el terreno ya que sólo se dispone de recursos inmediatos por M$4000. Formule y resuelva gráficamente utilizando el software Graphic Linear Optimizer (GLP) un modelo de Programación Lineal que provea el plan más eficiente de explotación, indicando claramente la solución óptima y valor óptimo.

El modelo de Programación Lineal para la situación anterior es:

Donde $x_{1}$ representa las hectáreas para talar y dejar para uso agrícola y $x_{2}$ las hectáreas para talar y plantar pino. En la siguiente imagen se muestra un extracto de la interfaz del programa GLP donde al pie de la misma se observa la solución óptima del problema con $x_{1}=25$ y $x_{2}=75$ . El valor óptimo es 6.250 el cual se encuentra en la fila con la etiqueta PAYOFF.

El software GLP permite ajustar tanto la escala del gráfico como un zoom personalizado en cualquiera de los ejes de coordenadas. No obstante recomendamos hacer uso de la funcionalidad Auto Zoom que ajusta automáticamente la representación gráfica a una escala adecuada en relación a la magnitud de los datos de origen.

A continuación dejamos a nuestros usuarios un enlace de descarga del software Graphic Linear Optimizer o GLP para que puedan probar sus distintas funcionalidades.

[sociallocker]

MUCHAS GRACIAS!. DESCARGA AQUÍ EL ARCHIVO

[/sociallocker]

Criterios para la Rapidez de Convergencia del Método Simplex

En un artículo previo respecto a Cómo resolver un modelo de Programación Lineal con el Método Simplex de 2 Fases, se consideró en una iteración intermedia (es decir, en un tableau que representa una solución básica factible no óptima) la entrada a la base de una variable no básica que no era aquella con el costo reducido más negativo. Dicha situación por cierto no tuvo incidencia respecto a alcanzar los resultados del modelo en cuanto a su solución óptima y valor óptimo, no obstante, dicha situación afecto la rapidez de convergencia del Método Simplex.

Entendemos por rapidez de convergencia en este caso, el número de iteraciones necesarias en la aplicación del Método Simplex para, comenzando en una solución básica factible inicial llegar a una solución básica factible óptima.

Se debe destacar que si bien es frecuente que en la bibliografía básica asociada a cursos de Investigación de Operaciones se considere como criterio privilegiar la entrada a la base de aquella variable no básica con el costo reducido más negativo esto NO garantiza un menor número de iteraciones en el Método Simplex.

Ejemplo Criterio Costo Reducido Más Negativo en el Método Simplex

Como forma de corroborar lo anterior retomaremos el modelo de Programación Lineal que fue presentado en el artículo mencionado anteriormente:

La resolución del problema anterior se aborda a través del Método Simplex de 2 Fases, incorporando $X_{4}$ y $X_{5}$ como variables de exceso y $X_{6}$ y $X_{7}$ como variables auxiliares, de las restricciones 1 y 2, respectivamente. Esto da origen al siguiente problema de la Fase 1.

Luego de algunas iteraciones del Método Simplex se alcanza la siguiente tabla:

A continuación podríamos seleccionar como variable que ingresa a la base tanto a $X_{1}$ , $X_{2}$ o $X_{4}$ , al tener cada una de estas variables no básicas un costo reducido negativo.

Luego, y según lo descrito anteriormente, podemos privilegiar la entrada a la base de la variable $X_{2}$ que tiene el costo reducido más negativo. En consecuencia el mínimo cuociente se calcula en la columna de la variable $X_{2}$ , siendo éste: $Min\begin{Bmatrix}\frac{1/4}{1/4};\frac{1}{3/2}\end{Bmatrix}=2/3$ , por tanto $X_{1}$ deja la base. Se actualiza la tabla con esta nueva información obteniendo lo siguiente que representa el fin de la Fase I:

Eliminamos las columnas de las variables auxiliares $X_{6}$ y $X_{7}$ y adicionalmente actualizamos el vector de costos reducidos considerando la función objetivo original.

Luego llevamos a cero los costos reducidos de las variables $X_{3}$ y $X_{2}$ :

Ahora entra la variable $X_{1}$ a la base. El criterio de factibilidad o mínimo cuociente determina que $Min\begin{Bmatrix}\frac{1/12}{1/3};\frac{2/3}{2/3}\end{Bmatrix}=1/4$ la variable $X_{3}$ deja la base. Se actualiza la tabla:

Que corresponde a la tabla final de la Fase II donde $X_{1}=1/4$ , $X_{2}=1/2$ y $X_{3}=0$ y que por cierto demuestra la equivalencia en los resultados obtenidos cuando en la tabla intermedia de la Fase I se ingresa a la base a la variable $X_{1}$ . Cabe destacar que una forma alternativa de resolver el problema anterior que evita la aplicación de las 2 Fases del Método Simplex es a través del Método Simplex Dual.

Ejemplo Criterio Costo Reducido Negativo en el Método Simplex

Consideremos el siguiente problema de Programación Lineal:

El lector puede corroborar que luego de llevar a la forma estándar el problema anterior, pasando a minimización la función objetivo y agregando como variables de holgura las variables $x_{3}$ y $x_{4}$ se dispone de una solución básica factible inicial en el origen (vértice A de la siguiente gráfica).

Si se privilegia la entrada a la base de aquella variable no básica con el costo reducido más negativo se debería seleccionar inicialmente la variable $x_{2}$ la cual permite concluir con las iteraciones del Método Simplex y alcanzar la solución óptima al cabo de 3 iteraciones (vértice D). Por el contrario si inicialmente se ingresa a la base la variable $x_{1}$ se alcanza la solución óptima al cabo de 1 iteración. Se recomienda al lector verificar estos resultados.

Este sencillo ejemplo demuestra que NO necesariamente garantiza una mayor rapidez de convergencia del Método Simplex el considerar como criterio de entrada a la base aquella variable no básica con el costo reducido más negativo.

Cambio de Variables como alternativa al Método Simplex de 2 Fases

Una empresa que fabrica tres artículos A, B y C, desea encontrar un Plan de Producción semanal que le permita maximizar sus beneficios netos totales. Los productos son procesados en tres máquinas siendo la producción mínima semanal de 100, 60 y 60 unidades respectivamente. El beneficio neto por unidad vendida de estos artículos son 2, 2 y 4 mil pesos para los artículos A, B y C, respectivamente. Las horas que se necesitan por unidad y máquina son:

Siendo el número de horas disponibles de cada máquina 240, 400 y 360 respectivamente. Formule un modelo de Programación Lineal para abordar el problema propuesto. Resuelva a través del Método Simplex dicho modelo, indicando cuántas unidades de A, B y C se deben fabricar semanalmente y el beneficio final de este plan.

Variables de Decisión: Se debe definir cuántas unidades de cada uno de los 3 productos se fabricarán durante el período de evaluación.

Función Objetivo: Consiste en maximizar el beneficio neto asociado al plan de producción.

Restricciones: Se debe garantizar que se fabrique los mínimos semanales exigidos para cada producto como también que se respete la disponibilidad de horas máquinas.

El problema anterior se puede resolver por el Método Simplex de 2 Fases agregando variables de exceso y auxiliares para cada una de las restricciones que establecen los mínimos semanales de producción. Además se debe agregar variables de holguras para cada una de las restricciones de disponibilidad de horas máquinas. En consecuencia el problema de la Fase 1 tendría 3 variables auxiliares (cuya sumatoria se minimiza en la función objetivo) lo cual genera una instancia de resolución al menos tediosa para este problema (en caso se ser abordada manualmente).

Una alternativa más eficiente de resolución se alcanza al imponer un cambio de variables, lo que permite simplificar las restricciones de mínimos de producción semanal. Sea $X=A-100\geq 0$ , $Y=B-60\geq 0$ y $Z=C-60\geq 0$ . Luego $A=X+100$ , $B=Y+60$ y $C=Z+60$ , obteniendo la siguiente instancia de modelamiento equivalente:

A continuación llevamos a la forma estándar el modelo anterior, transformando la función objetivo a minimización y agregando $s_{1},s_{2},s_{3}$ como variables de holgura de las restricciones 1, 2 y 3, respectivamente:

Lo que da origen a la siguiente tabla inicial del Método Simplex:

A continuación incorporamos a la base a la variable Z considerando el criterio que favorece la rapidez de convergencia del algoritmo. Luego calculamos el criterio de factibilidad o mínimo cuociente en la columna de la variable Z: $Min\begin{Bmatrix}\frac{60}{2}; \frac{180}{1}; \frac{40}{1}\end{Bmatrix}=30$ , lo que determina que la variable $s_{1}$ deja la base. Se actualiza la tabla realizando una iteración del Método Simplex:

Se procede a incorporar a la variable $X$ a la base y $s_{3}$ abandona la base dado que $Min\begin{Bmatrix}\frac{150}{1}; \frac{10}{2}\end{Bmatrix}=5$ . Se realiza una iteración adicional que permite alcanzar la siguiente solución básica factible óptima:

La solución óptima es $X=5$ , $Y=0$ y $Z=30$ que al remplazar en las variables originales permite obtener $A=X+100=5+100=105$ , $B=Y+60=0+60=60$ y $C=Z+60=30+60=90$ . Notar que el valor óptimo es $V(P)=130+560=690$ luego de sumar el valor de la constante 560 al valor obtenido para la función objetivo del problema auxiliar. Se propone al lector corroborar los resultados anterior a través de la aplicación del Método Simplex de 2 Fases que por cierto permite alcanzar idénticos resultados pero con una mayor esfuerzo en la resolución.

Problema de Arriendo de Buses para Transporte de Pasajeros en Programación Lineal

El siguiente problema de Programación Lineal consiste en determinar una política óptima de arriendo de buses para el transporte de pasajeros que minimice los costos asociados a su arriendo y satisfaga los requerimientos de transporte y otras condiciones adicionales que se deseen imponer.

El Centro de Alumnos de Ingeniería Industrial de una respetada universidad desea celebrar el día del alumno en la playa. Este paseo está planificado para 1.200 alumnos como mínimo. Una empresa de transporte ofrece 2 tipos de buses pero solo cuenta con 28 conductores. La tabla de abajo indica la capacidad y el costo de arriendo de cada tipo de bus:

Para mantener el equilibrio de su flota, la empresa de transporte impone la condición de que el número de buses tipo B arrendados no puede exceder el número de buses tipo A arrendados. Formule y resuelva un modelo de Programación Lineal que permita determinar cuántos buses de cada tipo hay que arrendar para el paseo de modo que resulte lo más económico para el Centro de Alumnos.

Variables de Decisión:

$x$ : Cantidad de Buses Tipo A arrendados
$y$ : Cantidad de Buses Tipo B arrendados

Función Objetivo:

Minimizar $80.000x+110.000y$

Restricciones:

Cantidad de Alumnos: $40x+60y\geq 1.200$
Cantidad de Conductores: $x+y\leq 28$
Condición de Flota: $x-y\geq 0$
No Negatividad: $x,y\geq 0$

El dominio de soluciones factibles del problema esta dado por el polígono ABC según se detalla a continuación (representación gráfica realizada con el software Geogebra). En particular la solución óptima corresponde al vértice A donde $x=12$ e $y=12$ , con valor óptimo $V(P)=80.000*12+110.000*12=2.280.000$ .

Notar que si bien el problema fue modelado como uno de Programación Lineal, dadas las características del problema sería deseable obtener una solución entera para las variables de decisión (dado que no es posible arrendar una fracción de buses y asumir por ejemplo que el costo del mismo es proporcional a la capacidad ocupada). No obstante en el ejemplo propuesto la solución óptima obtenida cumple de forma natural con las condiciones de integralidad, lo que indica que sus resultados son idénticos al problema de Programación Entera asociado (es decir, aquel al cual se le agregan de forma explícita las condiciones de enteros para las variables de decisión).

De forma complementaria al análisis anterior se pueden responder las siguientes preguntas correspondientes al análisis de sensibilidad o postoptimal:

1. Determine cuánto podría variar el costo de arriendo del Bus tipo A que conserve la solución óptima. Si C1 (costo arriendo del Bus tipo A) varía en el intervalo entre [73.333,3 , ∞[ se conserva la actual solución óptima.

2. Determine el impacto en el valor óptimo del problema si se elimina la condición que el número de buses tipo B arrendados no puede exceder el número de buses tipo A arrendados. El precio sombra de la restricción de condición de flota es 4.000. Luego si se elimina la condición de flota la solución óptima se alcanza en la mínima variación $(x,y)=(0,20)$ para una reducción permisible del lado derecho de dicha restricción en 20 unidades. Luego el nuevo valor óptimo es $V(P)=2.280.000+(-20-0)*4.000=2.200.000$ .