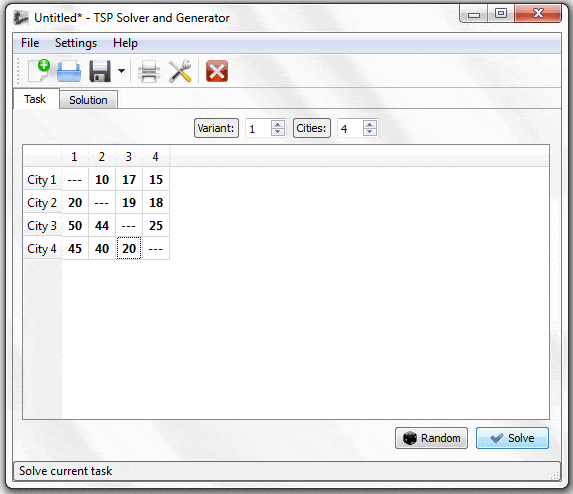
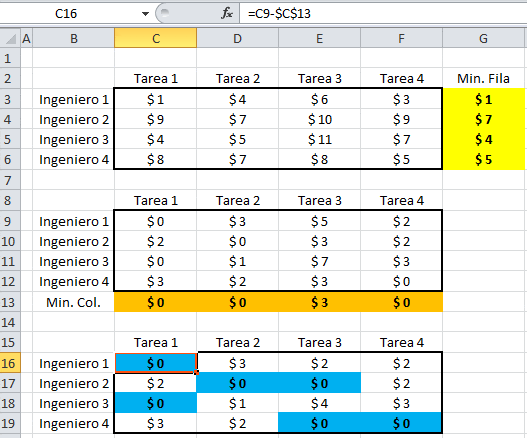
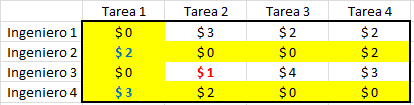
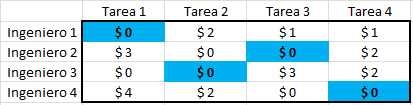
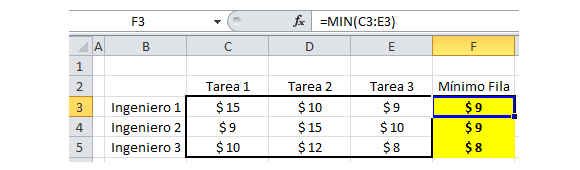
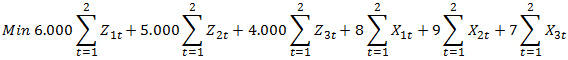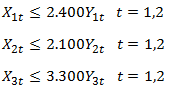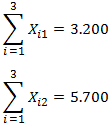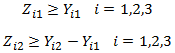programación entera Archivos - Página 4 de 9

Problema de Generación Eléctrica mediante Programación Entera Mixta

Una de las particularidades de los modelos de Programación Entera es que permiten incorporar en la representación matemática costos fijos que no son proporcionales al nivel de actividad en un sistema. Tal sería el caso, por ejemplo, de una empresa que desea determinar lotes de compra de un producto dado, en los que incurre en costos fijos asociados a la gestión de compra (independiente del volumen de unidades compradas dentro de los límites máximos impuestos por el proveedor) y costos variables (proporcionales) a la cantidad de unidades compradas. En este contexto se presenta a continuación un problema de generación de energía eléctrica donde se debe determinar la utilización y actividad de generadores que busca satisfacer requerimientos proyectados de energía de un día particular.

EGE abastece de electricidad a tres ciudades. La compañía dispone de cuatro generadores que son utilizados para proporcionar la potencia eléctrica requerida. El generador principal es empleado las 24 horas del día y no es materia de planificación en este problema.

Los otros tres generadores (que llamaremos 1, 2 y 3) están disponibles para generar la potencia adicional cuando se requiera. Considerar que se incurre en un costo de arranque cada vez que uno de estos generadores comienza a operar.

Los costos de arranque son de $6.000 para el generador 1, de $5.000 para el generador 2 y de $4.000 para el generador 3. Estos generadores se utilizan (por separado) únicamente de la siguiente manera: se puede poner en operación a las 6am y funcionar 8 horas (hasta las 2pm) o 16 horas (hasta las 10pm), o puede ponerse en funcionamiento a las 2pm y funcionar 8 horas (hasta las 10pm).

Los pronósticos para mañana indican la necesidad de contar con 3.200 MW adicionales entre las 6am y las 2pm, necesidad que se eleva a 5.700 MW entre las 2pm y las 10pm. El generador 1 puede proporcionar hasta 2.400 MW, el 2 hasta 2.100 MW y el 3 hasta 3.300MW. El costo por MW utilizado durante un periodo de 8 horas es de $8 en el caso del generador 1, $9 en el de el generador 2 y $7 en el caso del generador 3.

Formule y resuelva un modelo de Programación Entera Mixta para determinar los niveles óptimos de operación de cada generador para el día de mañana que minimice los costos totales satisfaciendo los requerimientos adicionales de potencia eléctrica.

Variables de Decisión:

Si bien se podría considerar cierta similitud en la definición de $Y_{it}$ y $Z_{it}$ , su utilización se justifica dado que el costo fijo de arranque se debe asociar precisamente a dicho concepto (puesta en marcha de un generador) el cual se produce (en caso de ser utilizado) sólo una vez durante el período de planificación.

Función Objetivo:

Se busca minimizar los costos fijos asociados al arranque de los generadores más el costo variable que resulte de la cantidad de MW aportados por éstos al sistema en los 2 tramos o períodos de planificación.

Restricciones:

Capacidad Generadores: La cantidad de MW que aporta cada generador al sistema no puede superar su capacidad máxima disponible (en caso que se emplee) en cada uno de los períodos de planificación.

Demanda MW: En conjunto los generadores deben aportar la cantidad de MW adicionales para cada tramo horario, es decir, de 6am a 2pm y de 2pm a 10pm.

Relación Arranque Funcionamiento: Un generador sólo podrá ser empleado si arranco en el período de planificación actual o inmediatamente anterior, en caso contrario el generador no arranca (y por tanto no funciona en ninguno de los 2 períodos).

No Negatividad: La cantidad que aporta cada generador en los 2 tramos horarios de 8 horas debe ser mayor o igual a 0 (MW).

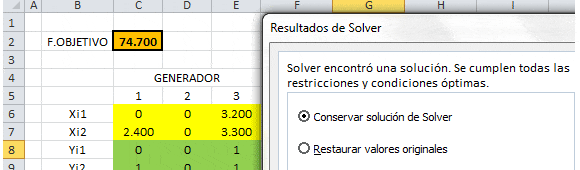
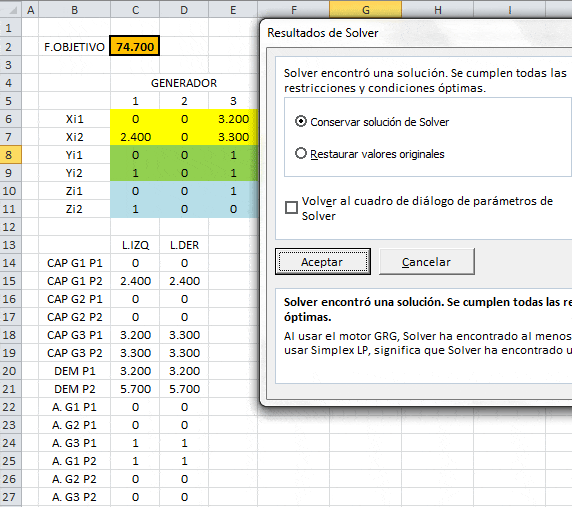
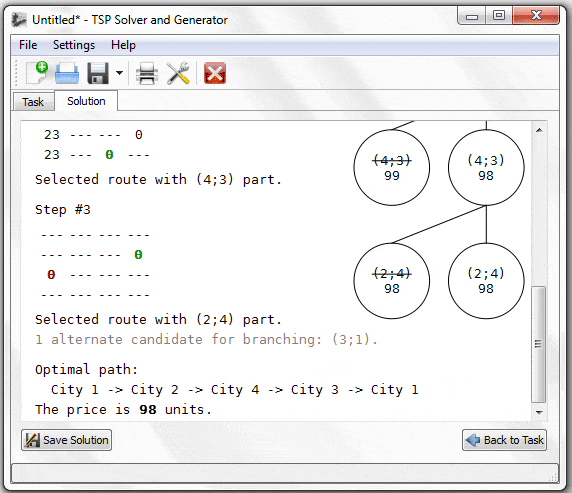
Al implementar el modelo anterior haciendo uso de Solver se alcanzan los siguientes resultados:

Notar que sólo arranca el generador 1 (a las 2 pm) y el generador 3 (a las 6 am). El generador 2 no arranca (y en consecuencia no se emplea) durante todo el día. El generador aporta 2.400 MW de 2pm a 10 pm, en tanto el generador 3 aporta con 3.200 MW de 6 am a 2 pm y 3.3o0 MW de 2 pm a 10 pm, respetando en cada caso las capacidadidas disponibles y satisfaciendo los requerimientos de demanda. Finalmente el costo óptimo (mínimo) es de $74.700.

Algoritmo del Plano de Corte en el Problema del Vendedor Viajero

Según lo descrito en el artículo Solución del Problema del Vendedor Viajero, una de las situaciones potenciales a la que nos podemos enfrentar es que la solución de asignación obtenida represente un subcircuito, lo cual naturalmente no da respuesta a la problemática que el modelo de agente viajero desea abordar. En este contexto existen diversas estrategias algorítmicas que permiten enfrentar esta situación entre las cuales destaca el Algoritmo de Plano de Corte.

La idea del Algoritmo del Plano de Corte es agregar un conjunto de restricciones que, cuando se incorporan al Problema de Asignación garanticen evitar la formación de un subcircuito. Consideremos un problema con n ciudades, asociar una variable continua $u_{j}\geq 0$ con las ciudades 2,3,…,n. A continuación definir un conjunto de restricciones adicionales de la siguiente forma:

Estas restricciones al añadirse al Modelo de Asignación, eliminarán todas las soluciones de subcircuito de forma automática, pero no eliminarán alguna solución de circuito.

A modo de ejemplo consideremos nuevamente el problema de secuenciamiento de la producción donde nos interesa determinar el orden en el cual se deben producir 4 colores de pintura.

A continuación se define un modelo de optimización haciendo uso del lenguaje de programación matemática AMPL. Para ello se puede utilizar un editor de texto como Bloc de Notas o WordPad. La siguiente imagen muestra la sintaxis utilizada en la definición del modelo del ejemplo propuesto donde se incorpora las restricciones que evitan los subcircuitos. Notar que es importante guardar el archivo con el formato adecuado (.mod) para lo cual simplemente en el caso de utilizar Bloc de Notas seleccionamos «Archivo», seguido de «Guardar como …» y luego en «Nombre» se ingresa un nombre arbitrario seguido de .mod (por ejemplo, modelo.mod).

El siguiente paso es generar un nuevo archivo con los datos o parámetros del problema. Básicamente aquellos que resumen el tiempo (en minutos) necesarios para la limpieza al realizar un cambio de colores, según se describe al inicio de este artículo. Notar que para evitar aquellas asignaciones infactibles (como que a un color le precede el mismo en la secuencia) se asignan «constantes grandes» a los elementos en la diagonal. El archivo se procesa y guarda de forma similar al caso del modelo pero con la extensión .dat (por ejemplo, matriz.dat).

Finalmente será necesario construir un tercer archivo con extensión .run que provee de instrucciones adicionales para efectos de la resolución computacional y que facilita la interpretación de los resultados (por ejemplo, solucion.run).

Una vez definido el modelo, datos y archivo run, podemos utilizar un solver de Programación Entera Mixta de los disponibles en el Servidor NEOS. En particular recomendamos utilizar el solver XpressMP donde se deberá adjuntar los archivos con extensión .mod, .dat y .run (respectivamente) según se muestra a continuación (recordar que el nombre asignado al archivo es arbitrario, no así su extensión).

Luego seleccionamos «Submit to NEOS» y los resultados se mostraran en el navegador de Internet, además de recibir un informe de respuestas en la dirección de correo electrónico que ingresamos. La siguiente imagen muestra un extracto de dichos resultados:

Notar que XpressMP encuentra como recorrido óptimo la secuencia 1-2-4-3-1, es decir, corresponde a producir en el siguiente orden: Blanco, Amarillo, Rojo, Negro, con un tiempo total de setup de 98 minutos.

Solución del Problema del Vendedor Viajero

El Problema del Vendedor Viajero (conocido también como Travelling Salesman Problem o simplemente TSP) consiste en encontrar el circuito óptimo (en términos del viaje más corto) que deberá seguir un vendedor en un caso con n ciudades, en el que cada ciudad se visita exactamente una vez. Básicamente es una adaptación del Problema de Asignación que considera restricciones adicionales que garantiza la exclusión de subcircuitos en la solución óptima.

Específicamente en el caso de n ciudades se define las variables de decisión de la siguiente forma:

Sea $d_{ij}$ la distancia de la ciudad i a la ciudad j, donde $d_{ij}=\infty$ , el modelo del agente o vendedor viajero corresponde a:

El conjunto de restricciones (1) y (2) definen un modelo de asignación tradicional. Lamentablemente en general, el problema de asignación producirá soluciones de subcircuito más que circuitos completos que abarque las n ciudades.

Para ilustrar los conceptos de circuito y subcircuito en el contexto del Problema del Vendedor Viajero, consideremos un agente de venta que vive en la ciudad 1. Miami (Florida) en Estados Unidos y debe visitar a importantes clientes en las siguientes ciudades: 2. Chicago (Illinois), 3. Houston (Texas), 4. Las Vegas (Nevada) y 5. San Francisco (California). Para mayor claridad se han destacado los estados mencionados anteriormente con un color distintivo.

Un circuito factible sería viajar en el siguiente orden: Miami (FL), Chicago (IL), Houston (TX), Las Vegas (NV), San Francisco (CA), Miami (FL). Es decir, $x_{12}=x_{23}=x_{34}=x_{45}=x_{51}=1$ .

Por otra parte un subcircuito correspondería, por ejemplo, a Miami (FL), San Francisco (CA), Las Vegas (NV), Miami (FL), junto a Houston (TX), Chicago (IL), Houston (TX). Es decir, $x_{15}=x_{54}=x_{41}=x_{32}=x_{23}=1$ , lo que naturalmente no es una solución factible para el problema que se busca resolver.

El modelo del vendedor viajero se caracteriza por su versatilidad para representar otros casos prácticos en optimización. Uno de ellos es el Problema de Secuenciamiento de la Producción como el que se presenta a continuación:

El programa de producción diaria de una empresa de pinturas incluye lotes de color Blanco (B), Amarillo (A), Negro (N) y Rojo (R). Como la empresa utiliza las mismas instalaciones en las cuatro clases de pintura, es necesario hacer una limpieza entre los lotes. La siguiente tabla resume el tiempo de limpieza, en minutos, donde al color de la fila sigue el color de la columna. Por ejemplo, cuando después de la pintura Blanca sigue la Amarilla, el tiempo de limpieza en 10 minutos. Como un color no puede seguir a sí mismo, a los elementos correspondientes se les asigna un tiempo de setup infinito. Se desea determinar la secuencia óptima para la producción diaria de los cuatro colores, que minimice el tiempo total de limpieza necesario.

Se puede hacer una analogía con el problema del vendedor viajero, asumiendo que cada pintura es una «ciudad» y que las «distancias» representan el tiempo de limpieza necesario para cambiar de un lote de pintura al siguiente. En consecuencia, el problema se reduce a determinar el circuito más corto que se inicie en un lote de pintura y pase exactamente una vez por cada uno de los tres lotes restantes, para regresar al punto de partida.

En este contexto dada la cantidad de pinturas, la secuencia óptima se puede encontrar por enumeración exhaustiva de los 6 circuitos posibles $(n-1)!$ , es decir, $(4-1)!=3!=6$ . En el ejemplo dicha secuencia óptima corresponde a Blanco, Amarillo, Rojo, Negro, Blanco, con un tiempo total de setup de 98 minutos. Naturalmente esta estrategia no es eficiente y queda limitada a problemas muy pequeños.

Alternativamente se puede utilizar implementar en Solver el modelo de asignación presentado anteriormente, haciendo uso de los parámetros descritos en el ejemplo del secuenciamiento de la producción de pinturas. A continuación un extracto de los resultados donde se observa que no se alcanza una solución de circuito.

En la actualidad existen programas computacionales que permiten enfrentar estas dificultades que establece el problema del vendedor viajero. Uno de ellos es el software TSPSG (TSP Solver and Generator) que se caracteriza por una interfaz intuitiva y que a continuación se detalla la implementación de nuestro problema (recordar que la Ciudad 1 correspondería al color Blanco, y así sucesivamente).

Una vez ingresado los datos al seleccionar «Solve» el programa se ejecuta entregando los resultados alcanzados que por cierto coincide con aquellos que identificamos por enumeración.

En términos algorítmicos los métodos disponibles para resolver el problema del agente o vendedor viajero tienen su base en las ideas de los algoritmos generales de ramificación y acotamiento (Branch and Bound) o de Plano de Corte, en los cuales abordaremos en próximos artículos.

Cómo enfrentar una Solución Infactible obtenida con el Método Húngaro

En algunos casos los ceros que se producen en los Pasos 1 y 2 del Método Húngaro no producen una solución factible en forma directa, es decir, la asignación alcanzada es infactible. En este caso se necesitan más pasos para alcanzar la asignación óptima (factible). Para ilustrar esta situación consideremos el siguiente ejemplo que consiste en la asignación a costo mínimo de 4 ingenieros a 4 tareas, donde cada ingeniero debe desempeñar exactamente una tarea:

Al aplicar los Pasos 1 y 2 del Método Húngaro se obtiene la siguiente matriz reducida:

Notar que los elementos cero (marcados con color azul) no permiten asignar una tarea por ingeniero. Por ejemplo, si se asigna el ingeniero 1 a la tarea 1, se eliminará la columna 1, y el ingeniero 3 no tendrá elemento cero en las tres columnas restantes. Para solucionar este obstáculo se agrega el siguiente paso al procedimiento:

Paso 2a: Si no se puede asegurar una asignación factible (con todos los elementos cero) con los Pasos 1 y 2.

Trazar la cantidad mínima de líneas horizontales y verticales en la última matriz reducida que cubran todos los elementos cero.
Seleccionar el elemento mínimo no cubierto, restarlo de todo elemento no cubierto y a continuación sumarlo a todo elemento en la intersección de dos líneas.
Si no se puede encontrar una asignación factible entre los elementos cero que resulten, repetir el Paso 2a. En caso contrario, seguir en el Paso 3 para determinar la asignación óptima.

Al aplicar el Paso 2a a la matriz reducida presentada anteriormente, se obtienen las celdas color amarillo según se aprecia a continuación:

La celda de valor mínimo sin fondo amarillo es igual a $1 (destacada con color rojo). Este elemento se resta de todas las celdas sin fondo amarillo y se suma a a las celdas de las intersecciones (destacadas con color azul).

La solución óptima (por cierto factible) se ha marcado con fondo azul: el ingeniero 1 realiza la tarea 1, el ingeniero 2 la tarea 3, el ingeniero 3 la tarea 2 y el ingeniero 4 la tarea 4 . El costo total (valor óptimo) de esta asignación es $1+$10+$5+$5=$21.

El Método Húngaro como Algoritmo de Solución del Modelo de Asignación

Un caso típico de un modelo de asignación es aquel que considera la asignación de trabajadores de distintos niveles de capacitación a puestos de trabajo. Naturalmente un puesto que coincide con los conocimientos de un trabajador cuesta menos que uno en el que el trabajador no es tan hábil. El objetivo del modelo es determinar la asignación de costo mínimo de trabajadores a puestos.

Consideremos un problema con n trabajadores que deben ser asignados a n puestos de trabajo. Sea $x_{ij}$ el costo de asignar al trabajador i al puesto j. Asumamos adicionalmente que cada trabajador debe realizar exactamente un trabajo. Notar que no existe pérdida de generalidad en asumir que la cantidad de trabajadores es igual a la cantidad de puestos, porque siempre se pueden agregar trabajadores o puestos ficticios para obtener esa condición.

El Método Húngaro consta de los siguientes pasos:

Paso 1: En la matriz original de costo, identificar el mínimo de cada fila y restarlo de todos los elementos de la fila.

Paso 2: En la matriz que resulte del Paso 1, identificar el mínimo de cada columna, y restarlo de todos los elementos de la columna.

Paso 3: Identificar la solución óptima como la asignación factible asociada con los elementos cero de la matriz obtenida en el Paso 2.

A continuación presentaremos un ejemplo que muestra la aplicación del Método Húngaro que nos permite decidir la asignación de trabajadores a puestos de trabajo.

Ejemplo Método Húngaro

Un equipo de 3 ingenieros debe ser asignado para la realización de 3 tareas, donde cada ingeniero debe hacer una tarea. Se requiere encontrar la asignación de costo mínimo para lo cual se dispone de los costos asociados a que el ingeniero i realice la tarea j. Por ejemplo, $c_{11}=15$ representa el costo correspondiente a que el ingeniero 1 asuma la tarea 1.

Aplicar el Método Húngaro para encontrar una asignación óptima de los ingenieros a las tareas.

El Paso 1 del Método Húngaro requiere identificar el valor mínimo de cada fila. En el caso de la fila 1 dicho valor es $9 siendo el costo de que el ingeniero realice la tarea 3. En particular si se dispone de un problema de mayor tamaño, hacer uso de Excel facilita los cálculos tal como se muestra en la siguiente imagen:

A continuación se resta el mínimo de cada fila a cada uno de los valores de la fila respectiva, para obtener la matriz reducida:

La aplicación del Paso 2 produce los mínimos de cada columna según se observa en la tabla anterior. Al restar esos valores de las columnas respectivas se obtiene la siguiente matriz reducida:

Las celdas con valor cero y color azul son la solución óptima. En consecuencia el ingeniero 1 realiza la tarea 2, el ingeniero 2 asuma la tarea 1 y el ingeniero 3 la tarea 3. Cada ingeniero realiza exactamente una tarea y el costo total de dicha asignación (valor óptimo) es de $9+$10+$8=$27. Los pasos presentados del Método Húngaro para el ejemplo anterior funcionaron bien debido a que los elementos cero de la matriz anterior permite una asignación factible de ingenieros a tareas (en el sentido que las tareas se asignan de forma única a los ingenieros). No siempre esto es posible lograr una solución factible en la aplicación caso en el cual se requiere pasos adicionales para la aplicación del método.