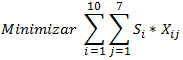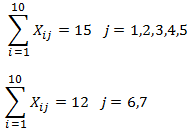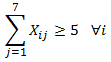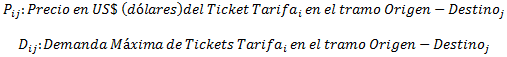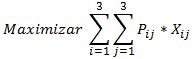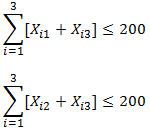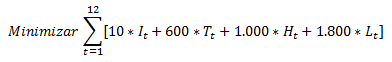tutoriales Archivos - Página 5 de 11 - Gestión de Operaciones

Problema de Asignación de Horas Académicas a Profesores aplicado a una Universidad Online

El desarrollo de las tecnologías de información ha favorecido un crecimiento sostenido en la oferta académica de las instituciones de educación superior, lo cual ha permitido sumar a la tradicional formación presencial la posibilidad de obtener grados académicos a través de una formación no presencial (online). En este contexto, en la actualidad existen numerosas «Universidades Online» las cuales deben programar horas de apoyo académico de sus distintos cursos por parte de los profesores o docentes hacia los alumnos, con el objetivo de favorecer la comprensión de los contenidos.

Problema de Asignación de Horas Académicas a Profesores

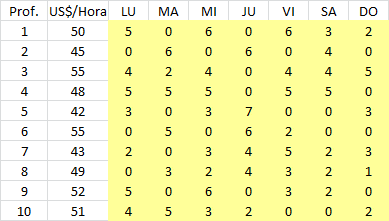
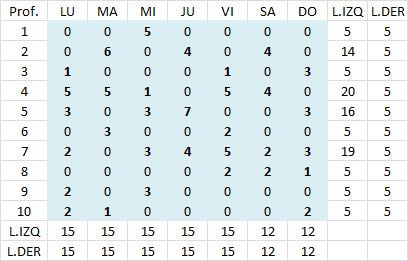
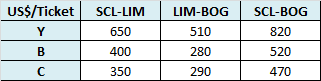
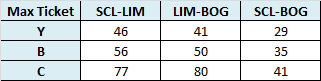
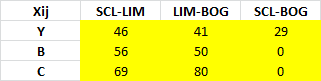
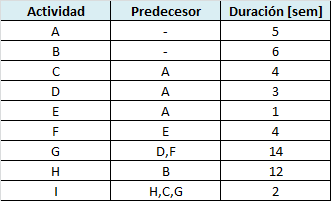
En el siguiente artículo consideraremos un problema de asignación para cubrir las necesidades de apoyo académico para un curso de Economía. Asumiremos que se desea tener exactamente un profesor de turno (para responder preguntas de los alumnos en tiempo real a través de un foro o chat) de Lunes a Viernes de 08:00 AM hasta las 23:00 PM. Los Sábados y Domingo también se desea ofrecer el servicio pero de 08:00 AM hasta las 20:00 PM. Actualmente se cuenta con 10 profesores que cuentan con los conocimientos necesarios para desarrollar los servicios de tutorias y su remuneración (en dólares por hora) depende básicamente de la experiencia en el curso y grado académico. Adicionalmente, debido a los compromisos que tienen dichos profesores con otros cursos de la Universidad, han manifestado su disponibilidad máxima (en horas) para atender los distintos requerimientos según se detalla en la siguiente tabla:

Por ejemplo el profesor 1 recibe un salario de 50 dólares la hora y puede trabajar como máximo 5 horas el Lunes, 6 horas el Miércoles y Viernes, 3 horas el Sábado y 2 horas el Domingo. Los días Martes y Jueves el profesor 1 no tiene disponibilidad de tiempo. En base a esta información la Universidad desea determinar una asignación de horas académicas a los profesores de modo de cubrir las necesidades de atención de alumnos al menor costo posible al mismo tiempo de garantizar un mínimo de 5 horas por profesor a la semana. Para enfrentar dicha situación formularemos el siguiente modelo de Programación Lineal:

Variables de Decisión:

Con i=1,…,10 representando a los profesores y j=1,…,7 los días de la semana don j=1 es el día Lunes y j=7 el día Domingo.

Parámetros:

Función Objetivo:

Se busca minimizar los costos totales de la asignación que considera la ponderación para cada profesor de la cantidad de horas que trabaja durante la semana por el salario por hora (en dólares).

Restricciones:

Se debe cumplir con la cantidad de horas para cada día de la semana (15 horas para cada día de Lunes a Viernes y 12 horas para el Sábado y Domingo).

Se desea asignar al menos 5 horas académicas semanales a cada profesor.

Se debe respetar la disponibilidad horaria de los profesores durante la semana.

Condiciones de no negatividad para las variables de decisión.

Luego de implementar computacionalmente el modelo de optimización con Solver de Excel se obtiene la siguiente solución óptima con valor óptimo V(P)=US$4.639.

El siguiente tutorial de nuestro canal de Youtube muestra la resolución del problema anterior:

Problema de Asignación de Capacidad de un Avión (Programación Lineal)

La industria de transporte de pasajeros enfrenta diariamente el problema de determinar cómo asignar de forma eficiente su capacidad de transporte al momento de ofrecer distintos tipos de tarifas a sus clientes para una ruta específica. Para ello se debe considerar de forma simultanea los ingresos por venta asociados a cada tipo de tarifa, una estimación de demanda de los clientes por dichas tarifas y la capacidad del medio de transporte en términos de la cantidad de asientos.

El siguiente problema considera la formulación y resolución computacional de un Problema de Asignación de capacidad de un avión para una empresa de transporte aéreo. La complejidad del problema y el nivel de detalle de la información se ha simplificado para fines académicos.

Problema de Asignación de Capacidad de un Avión

Consideremos una línea aérea que realiza la ruta Santiago (Chile) a Bogotá (Colombia) con escala en Lima (Perú). Para dicha ruta utiliza un avión con capacidad de 200 pasajeros. El departamento de ventas ha estimado los precios de mercado (en dólares) para las combinaciones de origen destino de 3 tipos de tarifas que actualmente ofrece la empresa: «Tarifa Y» (primera clase), «Tarifa B» (estándar) y «Tarifa C» (turista).

Adicionalmente y según información histórica de esta ruta, la línea aérea ha estimado el número máximo de pasajes que los clientes demandarán por cada combinación de tarifa en un tramo del vuelo. Por ejemplo la demanda máxima esperada para el tramo Santiago (SCL) a Bogota (BOG) en la Tarifa B es de 35 tickets.

Con esta información la línea aérea desea determinar cómo asignar la capacidad del avión de modo de ofrecer un determinado número de pasajes para cada tipo de tarifa en un tramo del vuelo. Para ello definiremos el siguiente modelo de Programación Lineal:

Variables de Decisión:

Donde i=1,2,3 representa los distintos tipos de tarifa (Y, B y C, respectivamente) y j=1,2,3 las combinaciones de origen destino (SCL-LIM, LIM-BOG y SCL-BOG, respectivamente).

Parámetros:

Al utilizar una notación con parámetros podemos representar el modelo de optimización de forma compacta.

Función Objetivo:

Restricciones:

Se ofrece para cada tarifa en las combinaciones origen destino un número de tickets que no supere la demanda máxima del mercado.

Para cada tramo del vuelo se debe respetar la capacidad total del avión de 200 pasajeros.

Cuando el avión despega desde Santiago con destino Lima lleva pasajeros con destino tanto a Lima como Bogotá. Por tanto independiente de la tarifa que cada uno de estos pasajeros haya pagado (por ello la sumatoria en las tarifas) no pueden superar la capacidad total del avión. Lo anterior esta garantizado por la primera restricción de capacidad.

La segunda restricción de capacidad es para el tramo desde Lima a Bogotá, donde se consideran adicionalmente los pasajeros que vienen desde Santiago.

Finalmente se definen las condiciones de no negatividad.

Al resolver con Solver el problema anterior se alcanza la siguiente solución óptima que determina cuántos pasajes debería ofertar la línea aérea para cada combinación de tarifa y origen destino.

El valor óptimo del problema que representa los ingresos totales (en dólares) asociados a la solución óptima propuesta es de US$158.340.

¿Quieres tener el archivo Excel con la resolución en Solver de este problema?.

[sociallocker]Descarga Aquí el Archivo[/sociallocker]

Cómo obtener la Ruta Crítica de un Proyecto (Critical Path Method)

El método de la Ruta Crítica conocida también por CPM por sus siglas en inglés (Critical Path Method) es una metodología de la Gestión de Proyectos que nos permite entre otros aspectos estimar la duración de un Proyecto. Para este propósito es necesario conocer las actividades que contempla el proyecto, su duración en una unidad de tiempo y el orden en el cuál deben ser realizadas (por ejemplo, algunas actividades se pueden desarrollar sólo cuando una o varias actividades previas o predecesoras han sido completadas).

Cómo obtener la Ruta Crítica de un Proyecto

El ejemplo a continuación muestra en detalle la aplicación del Método de Ruta Crítica a un proyecto que consta de 9 actividades cuyos tiempos estimados se encuentran en semanas. Adicionalmente en la columna «Predecesor» se establece el orden en el cual se deben realizar las distintas actividades, por ejemplo, la Actividad G se puede realizar una vez completada las Actividades D y F.

En este contexto resulta de utilidad desarrollar un Diagrama o Representación Gráfica del Proyecto donde cada nodo representa una actividad, el número al interior del paréntesis la duración de dicha actividad, y las flechas un camino o ruta consistente con las relaciones de precedencia.

Por ejemplo, la Actividad G tiene una duración estimada de 14 semanas y dicha actividad se puede iniciar una vez que hayan concluido sus predecesores, es decir, las Actividades D y F.

Se puede observar adicionalmente que las actividades iniciales son A y B y la actividad final es I.

Una actividad inicial es aquella que se puede comenzar inmediatamente y no existe ninguna otra actividad que le precede.
Una actividad final es una actividad que termina una ruta o camino del proyecto y en consecuencia no es predecesora de ninguna otra actividad del proyecto.

Por tanto la duración del proyecto estará determinado por aquella ruta o camino más largo que comenzando en una actividad inicial concluya en una actividad final. En nuestro ejemplo, un camino que comenzando en A (o en B) termine en I.

Luego, dado el tamaño reducido de este ejemplo es posible enumerar todas las posibilidades rutas o caminos que satisfacen la condición anterior:

Ruta: A-C-I: 5[sem]+4[sem]+2[sem]=11[sem]
Ruta: A-D-G-I: 5[sem]+3[sem]+14[sem]+2[sem]=24[sem]
Ruta: A-E-F-G-I: 5[sem]+1[sem]+4[sem]+14[sem]+2[sem]=26[sem]
Ruta: B-H-I: 6[sem]+12[sem]+2[sem]=20[sem]

La Ruta Crítica por tanto es A-E-F-G-I lo que determina que la duración del proyecto es de 26[sem].

Adicionalmente podemos estimar cuándo es lo más pronto que se puede comenzar cada actividad (inicio más cercano o IC – color rojo) y cuándo es lo más pronto que se puede terminar una actividad (término más cercano o TC – color azul).

Por ejemplo, para obtener el inicio más cercano y el término más cercano, en el caso de la Actividad A, éste será la semana 0 y 5, respectivamente. De la misma forma, lo más pronto que puede comenzar la Actividad C será en la semana 5 (tan pronto concluyo su predecesor que es la Actividad A) y lo más pronto que puede terminar es en la semana 9 (dado que la duración de la Actividad C es de 4 semanas) y así se continua el procedimiento desde el inicio hasta el final del proyecto.

En forma complementaria se puede obtener el tiempo más lejano en el cual se puede terminar una actividad sin atrasar el proyecto (término más lejano o TL – verde) y cuándo es lo más tarde que se puede comenzar una actividad sin retrasar el proyecto (inicio más lejano o IL – naranjo). Para obtener dichos tiempos retrocedemos desde la actividad final (I) hacia las actividades iniciales (A y B).

Por ejemplo, lo más tarde que puede terminar la Actividad H sin retrasar el proyecto es en la semana 24 (si termina más tarde de ello, entonces la Actividad I no se podrá iniciar en la semana 24 y por tanto el proyecto terminará más tarde que la semana 26). Naturalmente dado lo anterior, la Actividad H no podrá comenzar más tarde que la semana 12 si es que se desea terminar el proyecto en 26 semanas.

En este contexto se define el término Holgura (H) o Slack como el tiempo máximo que una actividad se puede retrasar en su inicio sin que esto afecte el tiempo estimado para terminar el proyecto como un todo:

Holgura = IL – IC = TL – TC

El siguiente diagrama muestra la ruta del proyecto con el cálculo de las holguras de cada una de las actividades. Se puede apreciar por ejemplo que la actividad B se puede retrasar un máximo de 6[sem] (su holgura) y aun así estar en condiciones de terminar el proyecto en 26[sem].

Adicionalmente las actividades que pertenecen a la ruta crítica tienen holgura igual a cero, lo que en este ejemplo en particular permite identificar una ruta única: A-E-F-G-I (notar que en general un proyecto puede tener más de una ruta o camino crítico).

Actualización: De forma de corroborar los resultados anteriores, a continuación se presenta una Carta Gantt del Proyecto obtenido a través del Método de Ruta Crítica (CPM). Con color rojo se destacan aquellas actividades que forman parte de la ruta crítica con holgura igual a cero.

Ejemplo del Problema del Camino Más Corto en Programación Entera

El Problema del Camino más Corto (o ruta más barata) consiste en encontrar una ruta o camino óptimo entre un nodo fuente y un nodo destino, los cuales están enlazados a través de una red con arcos que poseen un cierto atributo, el cual puede ser costo, distancia, tiempo, etc.

La Programación Entera permite abordar de forma eficiente este tipo de problemas, en especial cuando la cantidad de nodos y rutas posibles resulta ser un número significativo. Utilizar en estos casos un enfoque intuitivo de resolución es tedioso y de no ser exhaustivo no garantiza la identificación de la mejor alternativa o ruta.

Consideremos el siguiente diagrama donde los números asignados a cada uno de los arcos representan la distancia en kilómetros de un nodo a otro. Se desea encontrar la ruta con la distancia mínima para ir del nodo 1 al nodo 8.

El tamaño reducido de la red anterior permite encontrar el camino más corto simplemente enumerando las distintas alternativas que comenzando en el nodo 1 permita llegar al nodo 8. De esta forma las rutas posibles son:

Ruta 1-2-5-7-8: 4+8+17+9=38[km]
Ruta 1-3-4-7-8: 3+12+20+9=44[km]
Ruta 1-3-4-6-8: 3+12+2+22=39[km]
Ruta 1-3-4-8: 3+12+15=30[km]
Ruta 1-3-6-8: 3+4+22=29[km]

La ruta o camino más corto esta dada por la secuencia 1-3-6-8 con una distancia total de 29[km].

A continuación se formula un modelo de Programación Entera que permite extender este tipo de resultados a un problema de estas características:

Variables de Decisión:

Función Objetivo: Minimizar la distancia total en [km] dada por la siguiente expresión:

Restricciones:

La primera restricción (1) garantiza que sólo un nodo (entre el 2 y el 3) pueda ser el que se visita a continuación de comenzar en el nodo 1.
La restricción (2) determina que si se visito el nodo 2 después del nodo 1, entonces necesariamente el nodo 5 será visitado después del nodo 2.
La restricción (3) permite verificar que si el nodo 3 fue visitado luego del nodo 1, entonces a continuación se visita el nodo 4 o el nodo 6 (sólo uno de ellos).
La restricción (4) establece que si el nodo 5 fue visitado luego del nodo 2, entonces el nodo 7 debe ser visitado luego del nodo 5.
La restricción (5) garantiza que si el nodo 4 fue visitado luego del nodo 3, entonces a continuación se visita uno de los siguientes nodo: 7, 8 o 6.
La restricción (6) indica que si el nodo 6 fue visitado inmediatamente luego de estar en el nodo 3 o 4, a continuación se visita el nodo 8.
La restricción (7) determina que si el nodo 7 fue visitado inmediatamente luego de estar en el nodo 4 o 5, a continuación se visita el nodo 8.
Finalmente la restricción (8) asegura que ya sea el nodo 7, 4 o 6 sea el último en visitar previo a terminar la ruta en el nodo 8.

Al implementar en Solver el problema del Camino más Corto o Ruta Mínima anterior se alcanzan los siguientes resultados:

Donde se corrobora que la ruta más corta (solución óptima) corresponde al camino 1-3-6-8 con una distancia total de 29[km] (valor óptimo).

El tutorial a continuación disponible en nuestro canal de Youtube muestra en detalle la implementación y resolución computacional de este problema:

Formulación un modelo de Programación Entera para un Plan Maestro de la Producción (PMP)

La Planificación Agregada y el Plan Maestro de la Producción (PMP o MPS según sus siglas en inglés Master Production Schedule) son metodologías ampliamente utilizadas hoy en día en empresas de manufactura para planificar las necesidades de producción de una serie de productos, de modo de responder a un pronóstico de demanda a través de los recursos productivos que se disponen.

En este contexto, la evidencia empírica muestra que existen diversas estrategias que se pueden utilizar para enfrentar la demanda, cada una de las cuales se puede valorar en términos de costos pero también a través de una serie de criterios cualitativos que por su naturaleza son difíciles de estimar en una unidad monetaria.

A continuación se presenta un gráfico con el Pronóstico de Demanda de un producto para el cual propondremos un modelo de optimización que permita cumplir con dichos requerimientos, minimizando los costos asociados a la utilización de los recursos productivos:

Se puede apreciar que la demanda presenta una estacionalidad marcada donde al inicio y final del año los valores son menores a la demanda de un mes promedio (7.817 unidades).

En contraste con lo anterior en los meses de Junio, Julio y Agosto se presenta un peak de demanda, superando en magnitud claramente lo que correspondería a la demanda de un mes promedio. Adicionalmente consideremos los siguientes antecedentes de operación:

Costo de Contratar un Trabajador: US$1.000
Costo de Despedir un Trabajador: US$1.800
Costo de Almacenamiento Unitario Mensual: US$10
Inventario Inicial: 500 unidades
Costo Remuneración (Sueldo) de un Trabajador al Mes: US$600
Número de Trabajadores al Inicio de la Planificación: 100
Unidades de Producto producidas por un Trabajador al Mes: 50

La pregunta inmediata es: ¿Cómo responder a la demanda pronosticada durante el período de planificación al menor costo posible?. Algunas posibles respuestas son:

Fuerza Laboral Exacta: Esto es mediante contratación y despido de trabajadores para responder de forma exacta a las necesidades de cada mes. Con esta alternativa se busca evitar la acumulación de inventario.

Acumulación y Liquidación de Inventario: Producir en mayor volumen en los meses de menor demanda de modo de acumular inventario para enfrentar los requerimientos adicionales de los meses de mayor demanda. Si se considera adecuado se puede utilizar esta alternativa buscando no afectar el tamaño de la fuerza laboral.

Por cierto también se puede utilizar una estrategia mixta o híbrida que mezcle por ejemplo características de las 2 opciones presentadas anteriormente. Este enfoque generalmente es el que permite alcanzar menores costos.

Adicionalmente cabe destacar que en un Plan Maestro de la Producción (PMP) se podrían considerar otras alternativas o variables de ajuste no consideradas en este ejemplo como la utilización de trabajadores en tiempo extraordinario, la subcontratación parcial de la producción, la eventual postergación de demanda, entre otras opciones.

Luego, en relación a los antecedentes de operación previamente detallados, un modelo de Programación Entera para el Plan Maestro de la Producción es:

1. Variables de Decisión:

2. Función Objetivo:

3. Restricciones:

Satisfacer la Demanda (Balance de Inventario): Donde Dt corresponde a la demanda pronosticada para el mes t (parámetros).

Balance Mano de Obra: La cantidad de trabajadores en operación en cada período corresponde a los trabajadores disponibles al final del mes anterior, más los contratados y menos los despedidos en el mes en curso.

Capacidad de Producción: La producción de cada mes se ve limitada por la disponibilidad de trabajadores y el rendimiento mensual (en unidades de producto) que cada uno de éstos tiene.

No Negatividad e Integralidad: Todas las variables de decisión deben adoptar valores no negativos y adicionalmente ser enteras.

El modelo anterior se puede implementar con Solver y What’sBest! obteniendo los siguientes resultados:

Implementación Computacional en Solver: Se alcanza una solución factible con valor en la función objetivo de US$1.468.700.

El detalle de la resolución la puedes revisar en el siguiente tutorial de nuestro canal de Youtube:

Implementación Computacional con What’sBest!: Se alcanza una solución factible con valor en la función objetivo de US$1.468.400, la cual es ligeramente inferior en costos a la solución obtenida con Solver.

La carga del modelo en What’sBest! y la obtención de los resultados anteriores se puede revisar en el siguiente tutorial de nuestro canal de Youtube:

[sociallocker]Problema PMP www.gestiondeoperaciones.net[/sociallocker]