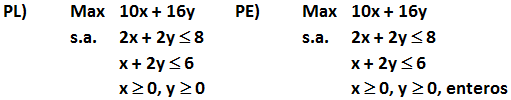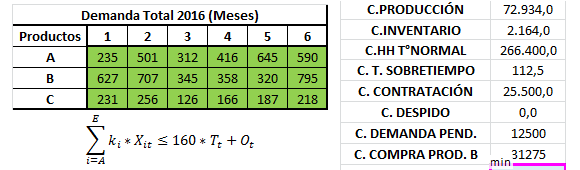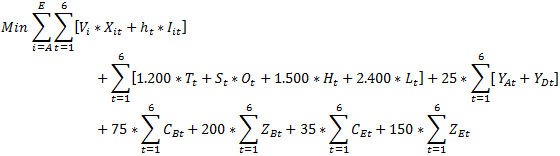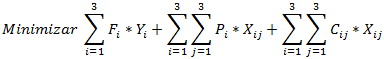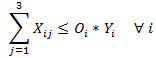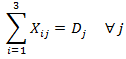programación entera Archivos - Página 2 de 9

Qué es la Programación Entera

¿Qué es la Programación Entera?: Un modelo de Programación Entera es aquel cuya solución óptima tiene sentido solamente si una parte o todas las variables de decisión toman valores restringidos a números enteros, permitiendo incorporar en el modelamiento matemático algunos aspectos que quedan fuera del alcance de los modelos de Programación Lineal.

En este sentido los algoritmos de resolución de los modelos de Programación Entera difieren a los utilizados en los modelos de Programación Lineal, destacándose entre ellos el Algoritmo de Ramificación y Acotamiento (o Branch & Bound), Branch & Cut, Planos Cortantes, Relajación Lagrangeana, entre otros.

Los modelos de Programación Entera se pueden clasificar en 2 grandes áreas: Programación Entera Mixta (PEM) y Programación Entera Pura (PEP).

Programación Entera Mixta (PEM)

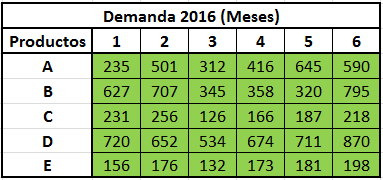
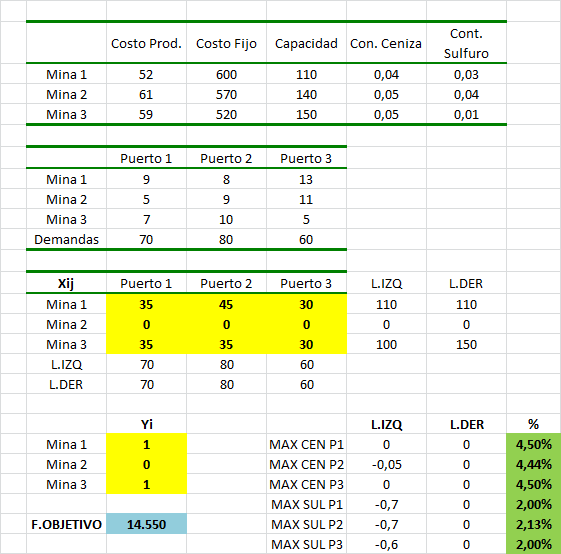
A esta categoría pertenecen aquellos problemas de optimización que consideran variables de decisión enteras o binarias pero no de forma exclusiva. De esta forma un problema de PEM puede considerarse como un híbrido entre distintas categorías de modelamiento, siendo un caso típico aquel que considera la mezcla de variables enteras y variables continuas (estas últimas características de los modelos de Programación Lineal). A modo de ejemplo los siguientes artículos que hemos abordado en el Blog dan cuenta de modelos de Programación Entera Mixta:

Programación Entera Pura (PEP)

En esta categoría encontramos aquellos modelos de Programación Entera que consideran exclusivamente variables de decisión que adoptan valores enteros o binarios. Un ejemplo de ello son las siguientes aplicaciones:

Problema de Asignación
Problema de Corte de Rollos
Selección de Invitados a una Boda
Programación de la Explotación Forestal
Problema de la Mochila

Notar que en los problemas anteriores (PEP) el conjunto de las soluciones factibles (o dominio de soluciones factibles) es finito. Esto ocurrirá generalmente con los problemas de Programación Entera (puros).

Adicionalmente resulta interesante hacer un contrastes entre las propiedades de un modelo de Programación Lineal (PL) y uno de Programación Entera (PE). A continuación se presentan 2 modelos de optimización que se diferencian únicamente en que al segundo de ellos (PE) se le exige que las variables de decisión adopten valores enteros.

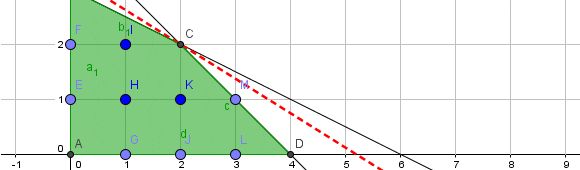
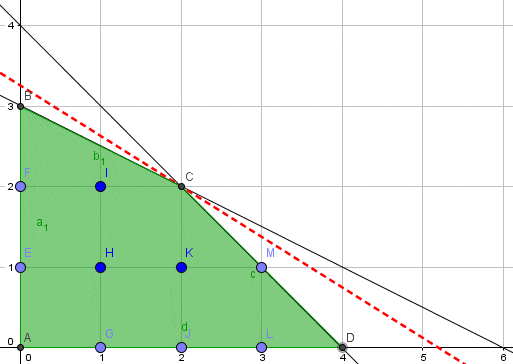
Para los problemas propuestos realizamos una representación gráfica haciendo uso del software Geogebra. El dominio de soluciones factibles del Problema Lineal (PL) corresponde al área achurada de color verde. Por otro lado el dominio de soluciones factibles del Problema Entero (PE) es enumerable y corresponde a las coordenadas denotadas por A, E, F, B, G, H, I, J, K, C, L, M, D (que es un subconjunto del dominio de factibilidad del PL). En este caso en particular la solución óptima de ambos problemas coincide (en el vértice C), no obstante, perfectamente podrían ser distintas (bastaría con modificar los parámetros del problema).

En este contexto y dada la naturaleza de los problemas propuestos, el valor óptimo del Problema Lineal (PL) será una cota superior del valor óptimo del Problema Entero (PE). También se concluye que el dominio de soluciones factibles de un modelo de Programación Lineal (cuando existe) representa un conjunto convexo (los problemas de Programación Lineal son convexos) y en el caso del problema de Programación Entera Pura su conjunto de soluciones factibles es discreto.

Adicionalmente según tratamos en el artículo Por qué no aparece el Informe de Confidencialidad (o Informe de Sensibilidad) en Solver de Excel se debe tener en cuenta que en la utilización de software para la resolución computacional del modelos de Programación Entera no tendremos acceso a los reportes de sensibilidad como en el caso de la implementación de modelos de Programación Lineal. De esta forma ante la necesidad de analizar el impacto en los resultados ante la modificación de los parámetros del problema será necesario reoptimizar ante la información que brinde el o los nuevos escenarios.

Es importante destacar que las aplicaciones de la Programación Entera no reemplaza la versatilidad que ofrece el disponer de modelos de Programación Lineal. Más aún, se pueden considerar estas categorías de modelamiento matemático como complementarias en el ámbito de la Investigación de Operaciones.

En este sentido en términos abstractos los modelos de Programación Entera imponen un desafío mayor al momento de la resolución en comparación a las propiedades simplificadoras que están asociadas a los problemas de Programación Lineal. De esta forma se espera que el tomador de decisiones sea capaz de evaluar la relación rigurosidad del modelado con el costo (complejidad) de la resolución del mismo.

Planificación de la Producción Multiproducto

El siguiente problema consiste en la formulación de un modelo de Programación Entera y posterior resolución computacional haciendo uso del complemento OpenSolver de Excel, específicamente en lo que se refiere a un modelo que permita encontrar la estrategia óptima para la Planificación de la Producción Multiproducto (es decir, 2 o más productos) y multiperiodo (2 o más períodos en el horizonte de evaluación). Referencias adicionales sobre esta clase de problemáticas pueden ser consultadas en la categoría Plan Maestro de la Producción (PMP) donde se presentan un importante volumen de ejercicios resueltos de planificación agregada. Dicho lo anterior a continuación presentamos el ejemplo objeto de nuestro análisis:

Una empresa desea optimizar la planificación de la producción de sus cinco productos principales para los primeros 6 meses del año 2016. Para el desarrollo de la tarea encomendada la empresa recolecta los siguientes antecedentes:

El proceso de fabricación es intensivo en mano de obra donde cada trabajador percibe un salario bruto de US$1.200 por una jornada de 160 horas de trabajo al mes.
El costo unitario de materiales y gastos generales, excluyendo el trabajo es de US$12 para A, US$14 para B, US$9 para C, US$13 para D y US$8 para E.
El costo de mano de obra de producción en tiempo extra se paga con un recargo de un 50% respecto a la hora trabajada en horario normal. No obstante por política de la empresa se establece un máximo de 200 horas hombre en tiempo extraordinario para cada mes, exceptuando Enero y Febrero donde el límite corresponde a 100 horas (por acuerdos con el sindicato).
El costo mensual de almacenar una unidad de cualquier producto en inventario es de US$4 por unidad. La bodega tiene una capacidad de almacenamiento de 250 unidades.
El tiempo de producción por unidad es de 5 horas para A, 6 horas para B, 8 horas para C, 4 horas para D y 3 horas para E.
La contratación de personal de producción considera un costo único de US$1.500 (adicional al sueldo) por concepto de capacitación y entrenamiento.
Para la reducción de horas de trabajo o despido considere en promedio: un sueldo de US$1.200 y una antigüedad de 2 años. Por política de estabilidad laboral se establece un máximo de despido de 6 trabajadores durante el primer semestre.
El inventario inicial corresponde a 120 y 80 unidades para los productos B y C respectivamente. No se dispone de inventario inicial para el producto A, D y E.
La planilla de trabajadores al 31 de Diciembre de 2015 es de 55 trabajadores.
Es posible dejar demanda pendiente del producto A y D asumiendo un costo unitario de US$25 en cada caso, la cual no expira y sólo se posterga para un próximo mes. No obstante la empresa requiere que como máximo queden 500 unidades de demanda pendiente (en total para la suma de ambos productos) a fines de Junio de 2016.
En cuanto al producto B, éste se puede comprar adicionalmente a un proveedor a un costo unitario de US$75. Adicionalmente el costo fijo de gestionar un pedido al proveedor del producto B (independiente del tamaño del pedido) es de US$200.
En cuanto al producto E, éste se puede comprar adicionalmente a un proveedor a un costo unitario de US$35. Adicionalmente el costo fijo de gestionar un pedido al proveedor del producto E (independiente del tamaño del pedido) es de US$150.

Formule y resuelva un modelo de optimización matemática que permita determinar la política operacional que minimice los costos totales en el horizonte de planificación y cumpla con las condiciones expuestas.

Planificación de la Producción Multiproducto

Variables de Decisión:

Notar que se dispone de 5 productos y 6 períodos. En este contexto y con el objetivo de lograr una notación más compacta se utilizan los índices i y t para representar los productos y períodos (meses), respectivamente.

Parámetros:

La definición de parámetros no es estrictamente necesaria y se realiza de modo de establecer un caso más general para el problema que facilita (compacta) la notación requerida para definir el modelo. Se puede apreciar que no todos los datos factibles de poder representar con parámetros ha sido llevado a cabo, lo cual corresponde a una decisión arbitraria la que sin embargo no afecta los resultados.

Función Objetivo:

Se busca minimizar los costos totales de la planificación multiproducto y multiperiodo. Los costos involucrados son (en orden): producción, inventario, mano de obra en tiempo normal, mano de obra en sobretiempo, contratación, despido, demanda pendiente, compra del producto B y compra del producto E.

Restricciones:

Balance de Inventario: Para el caso del producto A y D se puede utilizar demanda pendiente y para los productos B y E se pueden realizar compras. En este caso sólo los requerimientos del producto C deben ser satisfechos de forma exclusiva a través de la producción e inventario.

Balance de Trabajadores: La cantidad de trabajadores disponibles en un mes para funciones de producción será igual a los disponibles en el mes anterior, más los contratados en el mes y menos los despedidos en dicho mes.

Capacidad de Producción: El lado izquierdo de la restricción representa la cantidad de horas requeridas en un mes para la producción de los 5 productos, lo cual no podrá superar las horas disponibles (siendo éstas las horas en tiempo normal más las horas que eventualmente se utilicen en sobretiempo).

Capacidad de la Bodega: Para cada mes del horizonte de planificación la cantidad de productos almacenados en inventario (suma de todos los productos) no podrá superar la capacidad de almacenamiento de la bodega de 250 unidades.

Máximo de Compras B y E: La cantidad máxima de compra para el producto B y E dependerá si se adopta la decisión de realizar una compra en el mes respectivo. En dicho caso la cantidad máxima a comprar corresponderá a los parámetros o constantes grandes $M_{B}$ y $M_{E}$ , respectivamente. Por ejemplo un valor para $M_{B}$ podría ser 3.152 que corresponde a la suma de la demanda del producto B del mes 1 al mes 6.

Máxima Cantidad de Despidos: Durante el horizonte de planificación no se pueden despedir más de 6 trabajadores.

Máximo Demanda Pendiente Mes 6: Al final del mes 6 no debe quedar más de 500 unidades de demanda pendiente para el producto A y D (en conjunto).

No Negatividad y Enteros: Las variables de decisión deben adoptar no negativos y enteros (exceptuando las variables binarias).

La implementación computacional con OpenSolver del modelo de optimización anterior entrega los siguientes resultados. Las celdas en color amarillo corresponden a las variables de decisión del problema definidas inicialmente que satisfacen las restricciones impuestas (solución factible).

El valor óptimo corresponde a US$599.770 que corresponde al costo mínimo asociado al plan de producción. A continuación se desglosa dicho costo total en los distintos ítems de costos según lo detallado anteriormente.

¿Quieres tener la planilla Excel con la resolución en OpenSolver de este problema?.

[sociallocker]

MUCHAS GRACIAS!. DESCARGA AQUÍ EL ARCHIVO

[/sociallocker]

Formulación de un Problema de Programación de Explotación Forestal resuelto con Solver de Excel

En el artículo Problema de Planificación Forestal resuelto con Graphic Linear Optimizer (GLP) describimos un problema de explotación forestal reducido en términos de la complejidad de un caso de esta naturaleza (de modo de representarlo gráficamente), el cual a continuación extenderemos a través de la incorporación de una serie de decisiones en el tiempo respecto a la actividad de producción, planificación de personal, gestión de inventarios, compra, entre otros. En este contexto considere el caso de una compañía forestal que cosecha (tala) árboles los primeros meses del año. La compañía tiene una serie de pedidos que debe satisfacer cada mes. Estos datos se resumen a continuación:

Al 1 de Enero hay un total de 40 trabajadores y no hay árboles en inventario. La jornada laboral es de 40 horas semanales y 4 semanas laborales al mes. Para cosechar un árbol se requiere 4 horas hombre. Independiente de lo anterior la forestal tiene una capacidad de cosecha de 3.000 árboles mensuales lo cual está dado por la maquinaria disponible.

El sueldo mensual de cada trabajador es de M$400 (el sueldo se paga de forma íntegra ante todo evento, es decir, trabajando la totalidad de horas al mes o menos). La política de la gerencia es no utilizar horas extraordinarias pero si podría comprar árboles a otra forestal cercana a un costo unitario de M$18. Adicionalmente se ha convenido no contratar trabajadores por una fracción de una jornada de trabajo normal (160[horas/mes]). Esto implica que si se contrata un trabajador debe ser por 160[horas/mes] a un costo de M$400 pero no es válido, por ejemplo, contratar un trabajador por 80[horas/mes] a un costo de M$200. El costo de contratar un trabajador es de M$200 y el costo de despedir un trabajador se estima en M$600.

Almacenar un árbol en bodega tiene un costo de M$10 de un mes a otro. Sin embargo, en la bodega no hay espacio para almacenar más de 500 árboles.

Formule y resuelva un modelo de Programación Entera para este problema que permita hallar una política óptima de explotación para la forestal. Indique claramente las variables de decisión del modelo y detalle explícitamente la función objetivo y cada una de las restricciones del modelo.

Variables de Decisión:

Donde t=1,…,6 con t=1 Enero y t=6 Junio.

Función Objetivo: Minimizar los costos durante el período de planificación asociado a las remuneraciones, contratación, despido, compra y mantenimiento de inventario (respectivamente).

Restricciones:

Balance de Trabajadores: Por ejemplo la cantidad de trabajadores disponibles al final del mes de Marzo para labores de cosecha son aquellos que terminaron trabajando al final del mes de Febrero, más los contratados en el mes de Marzo y menos los despedidos en Marzo.

Satisfacer Demanda de Árboles: Donde $D_{t}$ representa la demanda (parámetros) de árboles para el mes t.

Capacidad Tala (Mano de Obra): Talar cada árbol requiere 4 horas hombre y un trabajador aporte 160 horas hombre en un mes. Luego, cada trabajador puede talar como máximo 40 árboles mensuales.

Capacidad Tala (Máquinas): Se puede talar como máximo 3.000 árboles mensuales dada la capacidad de las máquinas.

Capacidad Bodega: La bodega tiene una capacidad máxima de almacenamiento de 500 árboles.

No Negatividad y Enteros: Se deben satisfacer las condiciones de enteros para las variables de decisión no negativas.

Al implementar en Solver de Excel el modelo anterior se alcanza la solución óptima (celdas en color amarillo) con un valor óptimo de M$152.360.

Se recomienda al lector verificar que la solución alcanzada satisface las restricciones anteriormente expuestas. Notar adicionalmente que el plan óptimo actual no despide trabajadores durante la planificación y contrata trabajadores en Febrero y Abril (11 y 19, respectivamente), los mismos meses donde adicionalmente compra árboles (10 y 110) a la forestal cercana. Naturalmente al final de la planificación no existen incentivos para mantener árboles en bodega.

¿Quieres tener el archivo Excel con la implementación computacional de este ejemplo?

[sociallocker]

MUCHAS GRACIAS!. DESCARGA AQUÍ EL ARCHIVO

[/sociallocker]

Problema de Explotación de Minas y Transporte de Carbón a Puertos

Es frecuente reconocer en los problemas de optimización que representan una estructura productiva, un componente de costo fijo asociado a la utilización de un recurso (dentro de un intervalo de producción relevante) y un costo variable que que asume proporcional al nivel de actividad que represente la unidad productiva (por ejemplo, lo que se refiere a costos de producción, costos de transporte en una red logística, entre otros). Por ejemplo, el Problema de Inclusión de Costos Fijos en Programación Entera representa una situación muy sencilla de lo anteriormente descrito.

En este contexto a continuación se presenta un problema de operación de minas de carbón que su simple utilización tiene asociado un costo fijo, además de incurrir en costos variables por concepto de producción y transporte a distintos puertos demandantes, que adicionalmente tienen requerimientos particulares sobre la calidad del producto recepcionado.

Problema de Explotación de Minas y Transporte

La compañía ABC puede explotar hasta tres minas de carbón y debe realizar envíos a tres puertos. El costo por tonelada de producción (en dólares), el costo fijo de operación en dólares (en caso de ser utilizada), los contenidos de una cierta clase de ceniza y de sulfuro por tonelada y las capacidades de producción (en toneladas de carbón) se resumen en la siguiente tabla:

Por su parte, las toneladas demandadas que deben ser enviadas a cada puerto, conjuntamente con los costos de transporte (en dólares por tonelada) se dan en la siguiente tabla:

Formule y resuelva un modelo de optimización que permita determinar la eventual operación de cada mina y sus niveles de producción, de modo de satisfacer los requerimientos de demanda y que las cantidades enviadas a cada puerto contenga a los más un 4,5% de ceniza y a lo más un 3% de sulfuro.

Variables de Decisión:

Parámetros:

Función Objetivo: Se desea minimizar los costos asociados a la explotación de las minas, el costo de producción del carbón y los costos de transporte del carbón enviado desde las minas a los puertos.

Restricciones:

Capacidad de Producción de las Minas: cada mina puede operar a su capacidad máxima de producción para abastecer los requerimientos de los distintos puertos en caso en que se decida realizar funciones de explotación en la misma.

Demanda de Carbón los Puertos: cada puerto debe recibir la cantidad de toneladas de carbón que demanda.

Máximo Porcentaje de Ceniza admitido por cada Puerto: cada puerto esta dispuesto a recibir como máximo un 4,5% de ceniza en los envíos de carbón que recibe desde las minas. En este caso se expresa dicha condición de forma general a través de parámetros.

Máximo Porcentaje de Sulfuro admitido por cada Puerto: similar al caso anterior pero estableciendo un límite máximo al porcentaje de sulfuro que admite cada puerto (en el ejemplo un 3%).

No Negatividad: las toneladas producidas en las minas y transportadas a los puertos naturalmente deben satisfacer las condiciones de no negatividad.

A continuación de presenta un extracto de la implementación computacional del modelo anterior haciendo uso de Solver de Excel junto a un tutorial de nuestro canal de Youtube con los detalles de la resolución:

Se puede observar que sólo se utilizan las minas 1 y 3. La mina 1 envía 35, 45 y 30 toneladas al Puerto 1, 2 y 3, respectivamente. En el caso de la mina 3, ésta envía 35, 35 y 30 toneladas a los Puertos 1, 2 y 3, respectivamente. La demanda en toneladas de carbón es satisfecha en los puertos y se respeta adicionalmente la capacidad máxima de producción de las minas. Adicionalmente se puede observar en color verde el porcentaje de ceniza o sulfuro (según sea el caso) que recibe cada puerto lo cual satisface las condiciones expuestas. Finalmente el valor óptimo, es decir, el costo mínimo asociado al plan de producción y transporte descrito es de 14.550 dólares.

¿Quieres tener el archivo Excel con la implementación computacional de este problema?

[sociallocker]

MUCHAS GRACIAS!. DESCARGA AQUÍ EL ARCHIVO

[/sociallocker]

¿Cómo elegir los invitados de una Boda o Matrimonio con un modelo de Programación Entera?

Elegir los invitados a una boda (matrimonio) no es asunto fácil. Se debe respetar un presupuesto, cumplir compromisos familiares, compatibilizar los invitados de las distintas familias, incluir amigos y compañeros de trabajo y evitar incompatibilidades entre los invitados. El siguiente problema corresponde a una aproximación simplificada a la situación anterior a través de un modelo de Programación Entera. Por cierto las condiciones a incorporar en un problema de esta naturaleza pueden considerar aspectos adicionales como los comentados anteriormente.

Asuma que usted trabaja en una consultora matrimonial y su tarea es seleccionar los invitados para una boda. Tanto la novia como el novio están muy complicados porque tienen amigos que no pueden estar juntos. Los novios han asignado a cada invitado un valor en unidades matrimoniales (u.m) según lo siguiente:

Existen ciertas incompatibilidades que se deben considerar en la planificación que usted como consultor propondrá:

Juan Pérez no asistirá al menos que Luis Toro asista.
Juan Pérez no asistirá si tanto Pedro Soto y María González asisten.
Pedro Soto no asistirá si Gloria Pérez asiste.
Pedro Soto sólo asistirá si María González y Luis Toro asisten.

Formule y resuelva un modelo de Programación Entera que permita determinar a qué personas invitar de modo de lograr la mayor puntuación en unidades matrimoniales.

Variables de Decisión:

Con i=1,2,3,4,5 que representan a Juan Pérez, Pedro Soto, María González, Luis Toro y Gloria Pérez, respectivamente.

Función Objetivo:

Se desea encontrar la selección de invitados a la boda que permita maximizar la puntuación en u.m.

Restricciones:

Juan Pérez no asistirá al menos que Luis Toro asista: $X_{1}\leqslant X_{4}$
Juan Pérez no asistirá si tanto Pedro Soto y María González asisten: $2-(X_{2}+X_{3})\geq X_{1}$
Pedro Soto no asistirá si Gloria Pérez asiste: $X_{2}+X_{5}\leq 1$
Pedro Soto sólo asistirá si María González y Luis Toro asisten: $X_{2}\leqslant X_{3}$ y $X_{2}\leqslant X_{4}$ . En este conjunto de restricciones se entiende que si María González y Luis Toro asisten, Pedro Soto podría asistir. Si al menos uno de los 2 falta (María o Luis) entonces Pedro no asiste.

Al implementar el modelo anterior en Solver de Excel se alcanza un valor óptimo de 800 u.m el cual corresponde a invitar a Pedro Soto, María González y Luis Toro (solución óptima).