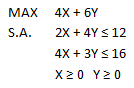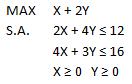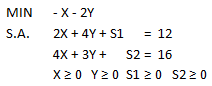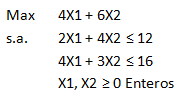GEO Tutoriales, Autor en Gestión de Operaciones

Interpretación del Informe de Sensibilidad de Celdas Cambiantes (Solver)

Cuando Resolvemos un modelo de Programación Lineal con Solver de Excel utilizamos una estimación de los parámetros (constantes) los cuales generalmente hacen referencia a disponibilidad de recursos, precios, costos, etc. En este contexto nos interesa simular el impacto en los resultados ante variaciones marginales de dichos parámetros sin la necesidad de resolver un nuevo modelo de optimización.

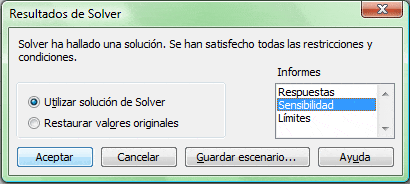
Este objetivo se puede alcanzar a través de los Informes de Sensibilidad de Solver los cuales se pueden generar una vez resuelto un escenario base para un modelo de optimización lineal, seleccionando la opción “Sensibilidad” (o Confidencialidad en versiones recientes de Office) según se muestra a continuación:

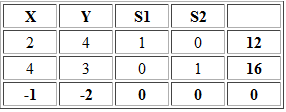
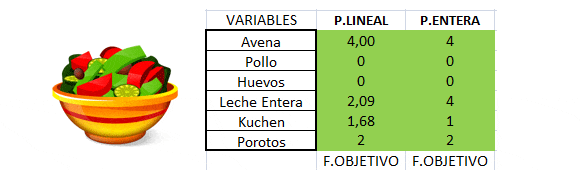
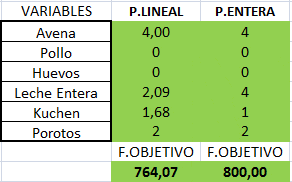
El siguiente análisis explica cómo interpretar el Informe de Sensibilidad de Celdas Cambiantes de Solver para el siguiente modelo de Programación Lineal:

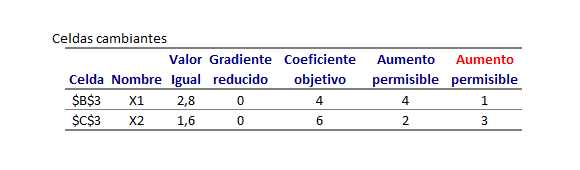
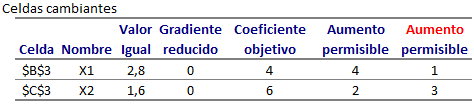
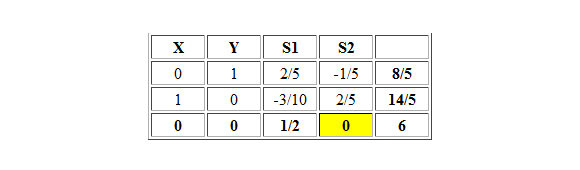
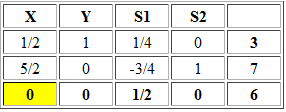
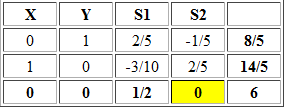
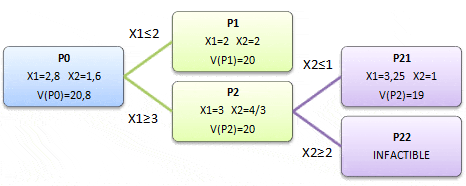
Con solución óptima X=14/5 Y=8/5 y valor óptimo V(P)=20,8. El Informe de Celdas Cambiantes corresponde a:

Notar que en la última columna se ha marcado con color rojo la palabra Aumento que debiese decir Disminución (este tipo de error se observa generalmente en las versiones más antiguas de Office).

El Informe de Sensibilidad de Celdas Cambiantes nos indica el intervalo de variación para cada parámetro de la función objetivo que permite mantener la actual solución óptima (asumiendo que el resto de los parámetros permanece constante).

Por ejemplo, el coeficiente que actualmente pondera a la variable X en la función objetivo de maximización es 4. El aumento permisible de 4 nos indica que el actual parámetro podría aumentar en dicha magnitud y la solución óptima actual se mantendría.

Análogamente se podría disminuir en 1 unidad (disminución permisible) y se conserva la solución actual.

En conclusión, el Intervalo de Variación para el parámetro que pondera a la variable X en la función objetivo que conserva la actual solución óptima es entre [3,8].

Siguiendo un procedimiento similar se puede demostrar que el intervalo de variación para el parámetro asociado a la variable Y en la función objetivo que conserva la actual solución óptima es entre [3,8] (sólo es una coincidencia que sean los mismos intervalos para cada parámetro).

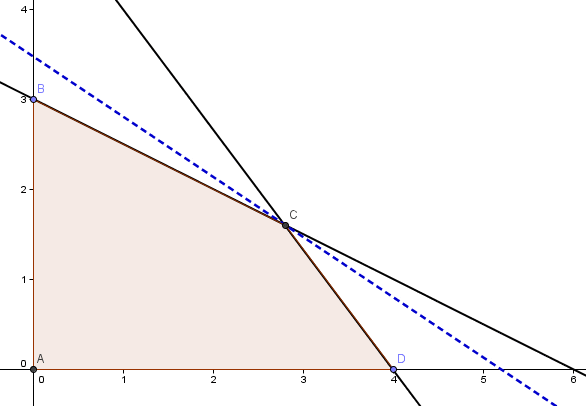
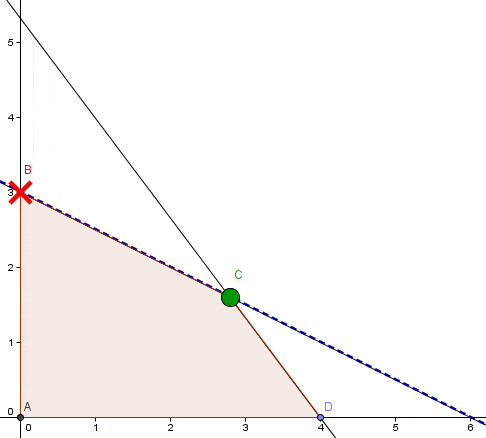
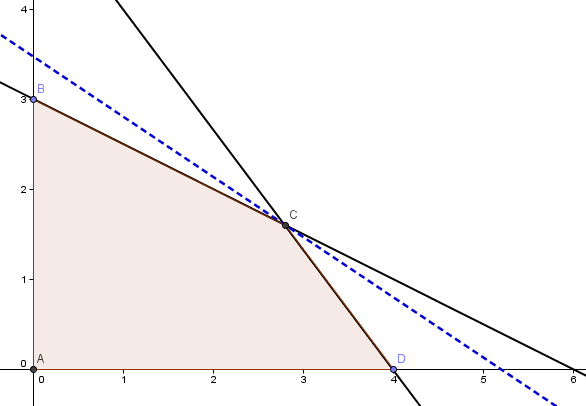
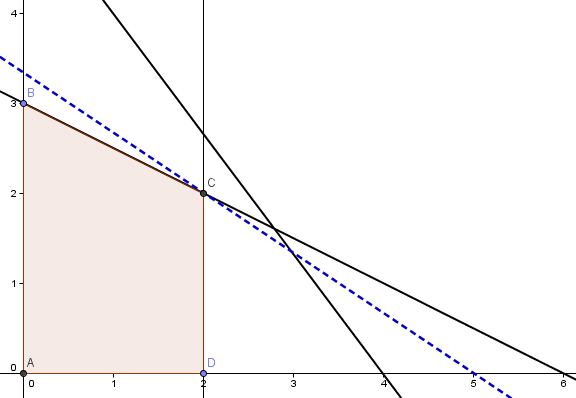
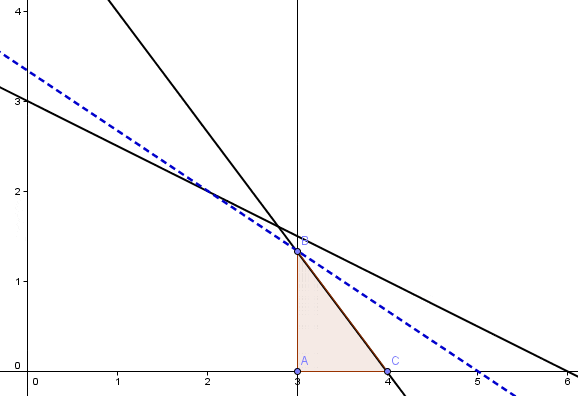
Por ejemplo, un cambio en uno de los parámetros de la función objetivo afecta la pendiente de ésta (curvas de nivel) que en la medida que se encuentre en el intervalo de variación previamente determinado mantendrá al vértice C como solución óptima del problema.

Una forma sencilla de corroborar estos resultados es mediante el Método Gráfico en Programación Lineal. Adicionalmente en el artículo Análisis de Sensibilidad Método Gráfico se detalla el procedimiento para obtener los intervalos de variación para los parámetros tanto en la función objetivo como en las restricciones del problema. Recomendamos revisar ambos artículos de modo de favorecer la comprensión de este tipo de análisis.

Cómo detectar Infinitas Soluciones con el Método Simplex

Una de las posibilidades a las que nos podemos enfrentar cuando resolvemos un modelo de Programación Lineal a través del Método Simplex es el caso de múltiples o infinitas soluciones óptimas.

Esto significa que existe un tramo de soluciones factibles que reportan idéntico valor para la función objetivo y que no es posible mejorar.

En este contexto si luego de aplicar las iteraciones que resulten necesarias por el Método Simplex a un modelo de Programación Lineal (tabla óptima o tableau óptimo) se verifica que una variable no básica óptima tiene costo reducido igual a cero, esto permitirá afirmar que estamos ante el caso de infinitas soluciones.

Ejemplo Infinitas Soluciones Óptimas Método Simplex

Consideremos el siguiente modelo de Programación Lineal:

Llevamos el modelo a su forma estándar para proceder con la aplicación del Método Simplex, con S1 y S2 como variables de holgura de la restricción 1 y 2, respectivamente.

La tabla inicial con S1 y S2 como variables básicas iniciales es:

Y entra a la base. Luego para determinar la variable que deja la base utilizamos el criterio del mínimo cuociente: Min {12/4 ; 16/3} = 3 ==> S1 deja la base. Con esta información actualizamos la tabla realizando operaciones fila:

Luego de una iteración encontramos la solución óptima, donde Y y S2 son variables básicas. La solución básica factible óptima es X=0 Y=3 S1=0 S2=7. El valor óptimo es V(P)=6.

Notar que X (variable no básica) tiene costo reducido igual a cero lo que determina la existencia de múltiples o infinitas soluciones óptimas, de modo que la solución actual es uno de los vértices óptimos.

El siguiente diagrama muestra la Resolución Gráfica del problema con el software Geogebra donde la solución óptima que hemos encontrado en la aplicación del Método Simplex corresponde al vértice B.

Notar que la línea punteada de color azul corresponde a una curva de nivel de la función objetivo que tiene la misma pendiente que la restricción 1 (pendiente -1/2).

¿Cómo podemos obtener el vértice C que es solución óptima a través del Método Simplex? Una alternativa sería forzando la entrada a la base de la variable X en la tabla óptima. Luego calculamos cuál de las actuales variables básicas deja la base según el criterio del mínimo cuociente: Min {3/1/2 ; 7/5/2} = 14/5 ==> S2 deja la base. Actualizando la tabla obtenemos:

La nueva solución óptima (con idéntico valor óptimo) es X=14/5 Y=8/5 S1=0 S2=0, que corresponde al vértice C en el gráfico anterior. Ahora la variable no básica S2 tiene costo reducido igual a cero en la tabla óptima que señala el caso de múltiples soluciones óptimas (en este ejemplo el tramo BC).

Regla de Jackson en la Programación de n Trabajos en 2 Máquinas

A diferencia de la Regla de Johnson aplicable a la programación de n trabajos en 2 máquinas bajo un esquema de atención fijo (es decir, los trabajos siguen siempre el mismo orden, por ejemplo primero pasan por la máquina A y luego por la máquina B), la Regla de Jackson (Método de Jackson) permite generar una Programación de Trabajos cuando la secuencia de dichos trabajos es aleatoria, es decir, se elimina el supuesto de que los trabajos siguen la misma secuencia.

En este contexto el Método de Jackson considera los siguientes pasos:

Paso 1: Clasificar los trabajos existentes en las 4 familias posibles: Los que requieren sólo la máquina 1 (A) – Los que requieren sólo la máquina 2 (B) – Los que pasan primero por máquina 1 y luego la 2 (AB) – Los que pasan primero por máquina 2 y luego la 1 (BA).
Paso 2: Ordenar los trabajos de (AB) y (BA) aplicando la Regla de Johnson.
Paso 3: Ordenar los trabajos de (A) y (B) en forma arbitraria.
Paso 4: Programar en la máquina 1 en primer lugar los trabajos de (AB), luego los trabajos en (A) y finalmente los trabajos en (BA).
Paso 5: Programar en la máquina 2 en primer lugar los trabajos de (BA), luego los trabajos en (B) y finalmente los trabajos en (AB).

Ejemplo Regla de Jackson

A continuación se presenta un ejemplo donde se deben programar 10 trabajos que tienen los siguientes tiempos y secuencias (Paso 1):

Paso 2: Los trabajos que siguen la secuencia A-B son el 1, 5, 6 y 9. El trabajo 9 es el más breve es en la máquina A por tanto se asigna y ejecuta en primer lugar. El trabajo 1 y 6 siguen con el tiempo más breve (10), sin embargo, el criterio de desempate nos indica que el trabajo 6 se asigna y ejecuta en segundo lugar. Posteriormente el tiempo más breve es en el trabajo 1 (máquina B) por lo cual se asigna este trabajo en tercer lugar y se ejecuta al último. La secuencia por tanto de los trabajos que siguen el orden A-B es: 9-6-5-1. Análogamente, siguiendo un procedimiento similar, los trabajos que siguen la secuencia B-A se ordenan 3-7-10 según la Regla de Johnson.

Paso 3: Los trabajos que sólo requieren la máquina A son el 2 y 8. De forma arbitraria seleccionaremos la secuencia 8-2. Finalmente existe un único trabajo que sólo requiere de la máquina B (trabajo 4).

Paso 4: La programación para la máquina A es: (9-6-5-1)-(8-2)-(3-7-10)

Paso 5: La programación para la máquina B es: (3-7-10)-(4)-(9-6-5-1)

Se propone a nuestros usuarios desarrollar una Carta Gantt considerando la secuencia anterior para ambas máquinas que permita encontrar el makespan asociado a dicha programación.

Ejemplo del Algoritmo de Branch and Bound (Ramificación y Acotamiento)

El método de Branch and Bound (o Ramificación y Acotamiento) es un algoritmo diseñado para la resolución de modelos de Programación Entera. Su operatoria consiste en linealizar el modelo de Programación Entera, es decir, resolver éste como si fuese un modelo de Programación Lineal y luego generar cotas en caso que al menos una variable de decisión (entera) adopte un valor fraccionario.

El algoritmo genera en forma recursiva cotas (o restricciones adicionales) que favorecen la obtención de valores enteros para las variables de decisión. En este contexto resolver el modelo lineal asociado a un modelo de Programación Entera se conoce frecuentemente como resolver la relajación continua del modelo entero.

Ejemplo Branch & Bound (Ramificación y Acotamiento)

Consideremos el siguiente modelo de Programación Entera el cual resolveremos con el algoritmo de Branch and Bound:

El paso inicial consiste en resolver este problema como si fuese un modelo de Programación Lineal (relajación continua). Si la solución de dicho problema llegara a respetar las condiciones de integralidad para las variables de decisión, ésta ya sería la solución óptima del problema entero.

Si bien este procedimiento se puede extender a problemas de mayor dimensión, utilizamos un modelo en 2 variables para poder representar los pasos del algoritmo gráficamente. El gráfico a continuación muestra dicha resolución:

La solución óptima del problema lineal asociado (que llamaremos P0) es X1=2,8 y X2=1,6 con valor óptimo V(P0)=20,8. Claramente esta solución no cumple las condiciones de integralidad para las variables de decisión por tanto es necesario generar cotas o restricciones adicionales de modo de poder obtener soluciones enteras. Para ello debemos seleccionar una de las 2 variables de decisión con valores fraccionarios para poder generar cotas. En estricto rigor es indistinto cuál de ellas seleccionemos debido a que el método nos debe llevar a conclusiones similares (aun cuando la cantidad de pasos requeridos o rapidez de convergencia cambie).

En nuestro ejemplo generaremos cotas adicionales para la variable X1 aproximando su valor actual al entero inferior más cercano (P1) y entero superior más cercano (P2).

La resolución gráfica del problema 1 (P1) nos da como solución óptima X1=2 y X2=2 que es una solución entera. El valor óptimo del problema 1 es V(P1)=20. Notar que V(P1)<V(P0) lo cual es natural dado que el dominio de soluciones factibles del P1 es menor (subconjunto) al dominio de soluciones factibles de P0.

Análogamente la resolución gráfica (Método Gráfico) del problema 2 (P2) determina que X1=3 y X2=4/3 con V(P2)=20 según se observa a continuación:

Luego no sería del todo necesario seguir desarrollando el algoritmo dado que si generamos cotas para la variable X2 del P2 en ningún caso podríamos obtener una solución entera con valor óptimo superior a 20 (valor que reporta en la función objetivo la actual solución entera de P1) y por tanto podríamos concluir que X1=2 y X2=2 es la solución óptima del problema entero. No obstante el siguiente diagrama muestra los pasos adicionales en caso que quisiera agregar cotas adicionales a partir del P2.

Un argumento similar al expuesto previamente en este caso explicaría la no necesidad de seguir ramificando el P21. Se propone al lector verificar que se obtiene la misma solución óptima si luego del P0 ramificamos a través de X2 agregando las restricciones X2<=1 y X2>=2.

Problema de la Dieta con variables enteras resuelto con Solver de Excel

En un artículo previo tratamos el Problema de la Dieta como una aplicación característica de la Programación Lineal discutido ampliamente en los Cursos de Investigación de Operaciones. El problema consiste básicamente en encontrar una combinación de alimentos óptima que permita satisfacer ciertos requerimientos nutricionales mínimos y adicionalmente tenga el menor costo asociado a la selección de los mismos.

Una vez obtenida la solución óptima y valor óptimo de dicho modelo nos podemos enfrentar al escenario donde todas o algunas de las variables de decisión adoptan valores fraccionarios. Si bien esta situación es aceptada en los modelos de Programación Lineal (en efecto constituye un supuesto básico de la Programación Lineal), puede resultar de interés simular una nueva solución donde las variables de decisión adopten valores enteros.

El siguiente tutorial muestra cómo incorporar las condiciones de integralidad al Problema de la Dieta, lo que da origen a un modelo de Programación Entera.

Se puede observar que hemos utilizado un formato similar al modelo de Programación Lineal, sin embargo, se incorpora la condición de integralidad para las variables de decisión como si fuese una restricción adicional. Adicionalmente en las Opciones de Solver debemos desactivar la selección de «Adoptar modelo lineal» debido a que ahora el modelo es de Programación Entera (esta indicación es válida para las versiones de Office 2007 y anteriores).

La tabla a continuación resume los resultados del Problema de la Dieta resuelto como un modelo de optimización lineal o entero:

Se puede observar que el valor óptimo del Problema Entero es superior al del Problema Lineal. Siendo éste un problema de minimización esta situación es natural dado que el dominio de soluciones factibles del problema entero está contenido en el dominio del problema lineal (es un subconjunto) y por tanto no podríamos encontrar nada mejor (más económico en este caso) que el valor óptimo del problema lineal.

Es importante destacar adicionalmente que para obtener la solución óptima de un problema entero NO es suficiente con aproximar los resultados fraccionarios del problema lineal asociado, por ejemplo, al entero superior o entero inferior más cercano. En consecuencia se requiere de algoritmos específicos para la resolución de modelos de Programación Entera, siendo el Algoritmo de Ramificación y Acotamiento (Branch & Bound) uno de los más populares.