GEO Tutoriales, Autor en Gestión de Operaciones

Pronóstico de Demanda con Alisamiento Exponencial para distintos Alfa (α)

El método de pronóstico de Alisamiento o Suavizamiento Exponencial pertenece a la categoría de Series de Tiempo, es decir, aquellos métodos donde se utiliza información de la demanda histórica para poder pronosticar el futuro. Su nombre se debe a que cada incremento del pasado se reduce en (1 – α) por lo cual se considera válido que la importancia de los datos disminuye en la medida que son más antiguos.

Para poder generar un pronóstico a través del método de Alisamiento Exponencial necesitamos el pronóstico más reciente, la demanda que se presentó para ese período y una constante de suavizamiento α (alfa).

El valor del parámetro alfa es entre 0 y 1. En esta escala para valores de alfa relativamente pequeños se reducen las variaciones de corto plazo asociadas al pronostico lo cual es razonable cuando la demanda real tiene un comportamiento relativamente estable. Sin embargo, si la demanda presenta cambios significativos en el corto plazo nos interesará seguir éstos más de cerca y en ese caso debiéramos seleccionar una constante alfa más grande.

Ejemplo Suavizamiento Exponencial

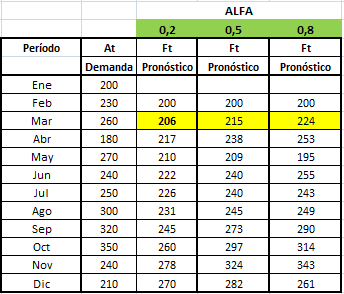
A continuación presentaremos 3 pronósticos para valores de alfa de α=0,2, α=0,5 y α=0,8. Los resultados se han aproximado (arbitrariamente y por comodidad) al entero más cercano. Notar que en cada caso el primer pronostico es de 200 (igual a la demanda real de Enero). Esta selección es usual dado que para la aplicación del método se necesita un primer pronóstico (o punto de partida) y frecuentemente se selecciona el dato real del período anterior:

En la tabla se puede apreciar que el pronóstico para el mes de Marzo utilizando α=0,2 es de 206. Esto se obtiene como F(Marzo)=200+0,2(230-200)=206. Siguiendo un procedimiento similar se puede calcular el resto de los pronósticos.

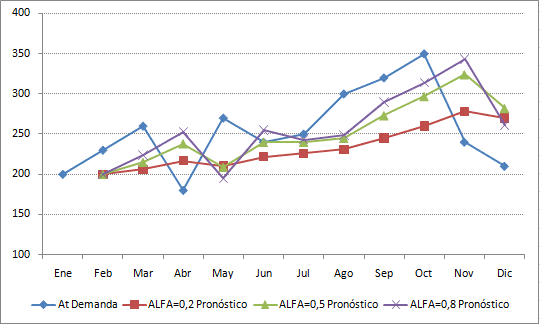
¿Cómo decidir que constante de suavizamiento alfa resultó mejor?. Un primer acercamiento es graficar el pronóstico y comparar su comportamiento con la demanda real. El siguiente gráfico representa esta situación. Se puede observar que para α=0,8 se replica de forma más cercana el comportamiento de la demanda aún cuando se aprecia un rezago (situación característica de este método). Por el contrario, para α=0,2 la variación de corto plazo es menor y el pronóstico básicamente marca una leve tendencia creciente. Finalmente para α=0,5 se obtiene un pronóstico intermedio entre los 2 escenarios anteriores.

En otro artículo discutimos como mediante el MAD y la Señal de Rastreo podemos simular y seleccionar una constante alfa en base a un criterio cuantitativo. Adicionalmente en la publicación Cómo utilizar el Módulo Predictor en Crystal Ball para Promedio Móvil Simple y Suavizado Exponencial Simple se muestra la aplicación del método de suavizamiento exponencial utilizando el software Crystal Ball.

Problema de la Dieta en Programación Lineal resuelto con Solver de Excel

Una de las aplicaciones clásicas de la Programación Lineal es el Problema de la Dieta. El objetivo es seleccionar un conjunto de alimentos dados que permitan satisfacer ciertos requerimientos nutricionales y preferencias y que adicionalmente tenga un costo mínimo.

En este contexto en el Servidor NEOS se puede encontrar un conjunto de antecedentes que permiten comprender el contexto histórico del Problema de la Dieta y cómo se puede abordar de forma eficiente a través de modelos de optimización. Al igual que varias de las aplicaciones de la Investigación de Operaciones este problema tiene un origen militar.

Para efectos de este tutorial y con el objetivo de ilustrar esta aplicación consideremos el siguiente listado de alimentos con su perfil nutricional y costo monetario:

Se desea proponer una dieta que contenga al menos 2.000 (Kcal) , al menos 55 gramos de proteína y 800 (mg) de calcio. Adicionalmente para garantizar cierta variedad en la dieta se establece límites de porciones por día en los alimentos. Con esta información se requiere encontrar la dieta que tenga el menor costo asociado y permita satisfacer los requerimientos anteriores.

Para ello definimos el siguiente modelo de Programación Lineal:

1. Variables de Decisión: Xi : Porciones de alimentos a consumir durante el día del alimento i (Con i=1 ==> Avena, …. i=6 ==> Porotos).

2. Función Objetivo: Minimizar 30X1+240X2+130X3+90X4+200X5+60X6

3. Restricciones:

Mínimo de Calorias (KCal): 110X1+205X2+160X3+160X4+420X5+260X6 >= 2.000
Mínimo de Proteínas: 4X1+32X2+13X3+8X4+4X5+14X6 >= 55
Mínimo de Calcio: 2X1+12X2+54X3+285X4+22X5+80X6 >= 800
Variedad de la Dieta: X1<=4 X2<=3 X3<=2 X4<=8 X5<=2 X6<=2
No Negatividad: Xi>=0 Para todo i.

La implementación de este modelo en Solver de Excel para obtener su solución óptima y valor óptimo se muestra en el siguiente tutorial:

La Solución Óptima es X1=4, X2=0, X3=0, X4=2,08, X5=1,68, X6=2 y el Valor Óptimo (costo de la dieta) es $764,07.

Como el modelo es de Programación Lineal se permiten valores fraccionarios para las variables de decisión. Por tanto si buscamos solo valores enteros para las variables de decisión en ese caso debemos definir un modelo de Programación Entera el cual revisamos en el siguiente artículo: Problema de la Dieta en Programación Entera resuelto con Solver de Excel.

Cantidad Económica de Pedido (EOQ) con Descuentos por Cantidad

Uno de los supuestos del modelo de Cantidad Económica de Pedido (o EOQ según sus siglas en inglés) es que el costo de adquisición unitario es independiente del tamaño del pedido, sin embargo, este supuesto es factible de flexibilizar debido a que en muchos casos es razonable asumir que se puede acceder a un determinado descuento por unidad en la medida de pedidos de tamaño mayor.

Para determinados productos, los proveedores suelen ofrecer una escala de descuentos dependiendo del tamaño del pedido. Este tipo de estrategia de venta es frecuentemente utilizado por mayoristas y distribuidores que buscan con esto tener una mayor Rotación de Inventario y en consecuencia disminuir los Días de Inventario (con la correspondiente disminución de los costos de almacenamiento del inventario). Adicionalmente, la escala de descuentos suele estar previamente tabulada y accesible para el comprador.

Ejemplo EOQ con Descuentos por Cantidad

A continuación tomaremos nuevamente los datos del ejemplo de EOQ analizados en el tutorial del Cálculo de la Cantidad Económica de Pedido con WINQSB, sin embargo, en esta oportunidad consideraremos que el costo de almacenamiento anual se puede representar como un porcentaje del costo de adquisición.

D: Demanda Anual = 6.000 unidades
S: Costo de Emisión = $750
H: Costo de Almacenamiento Anual (unitario) = 10% del costo de adquisición (i)

El precio unitario a pagar dependerá del tamaño del pedido según muestra la siguiente tabla:

Para poder determinar el tamaño de pedido que minimiza los costos totales se debe evaluar cada uno de los tramos de precios.

Notar que H=i*C, es decir, se considera que el costo de almacenar un producto se puede representar como un porcentaje de su costo de adquisición (compra). De esta forma, al aumentar los descuentos (y en consecuencia disminuir el precio de compra) el costo unitario de almacenamiento representado por H=i*C disminuirá y generará un incentivo a pedidos de mayor tamaño (dado que el denominador de la formula a continuación disminuye en magnitud).

En el primer tramo (sin descuento) el tamaño de pedido recomendado es de 150 unidades.

En el segundo tramo el tamaño de pedido óptimo según EOQ es de 160,3 unidades, sin embargo, dicho pedido es insuficiente para acceder al precio descontado de $3.500 por tanto para el tramo 2 el pedido óptimo se aproxima a 200 unidades.

Finalmente para el tercer tramo el tamaño del pedido es también insuficiente para acceder al precio unitario de $3.200 por tanto se aproxima a 300 unidades.

En resumen, para el tramo 1 ==> Q=150[u/ped]; tramo 2 ==> Q=200[u/ped]; tramo 3 ==> Q=300[u/ped].

Los fórmula de Costos Totales del Modelo EOQ es: CT=C*D+(D/Q)*S+(Q/2)*H

Tramo 1: CT=$4.000*6.000+(6.000/150)*$750+(150/2)*10%*$4.000=$24.060.000
Tramo 2: CT=$3.500*6.000+(6.000/200)*$750+(200/2)*10%*$3.500=$21.057.500
Tramo 3: CT=$3.200*6000+(6.000/300)*$750+(300/2)*10%*$3.200=$19.263.000

El menor costo se alcanza en el tramo 3 y la cantidad de pedido que minimiza los costos totales será de 300 unidades. Es importante destacar que no necesariamente el tramo con el menor precio unitario será el que tenga el menor costo asociado y por tanto el resultado obtenido en este ejemplo no se puede extrapolar para cualquier caso.

Cómo calcular Gráficamente el Precio Sombra de una Restricción

El Precio Sombra de una restricción en Programación Lineal indica cuánto cambia el valor de la función objetivo (óptimo) ante una variación marginal del lado derecho de una restricción. Se asume que el resto de los parámetros del modelo permanecen constantes. De antemano es conveniente señalar que el Precio Sombra puede ser positivo, cero o negativo y en el Blog iremos discutiendo estos distintos escenarios.

Para obtener los Informes de Sensibilidad de un modelo de Programación Lineal se puede hacer uso de herramientas computacionales como Solver de Excel, sin embargo, en esta oportunidad nos enfocaremos en el cálculo del precio sombra de una restricción en forma gráfica, lo que nos ayudará más adelante a entender los conceptos que fundamentan los resultados de Solver.

Cálculo del Precio Sombra de una Restricción con el Método Gráfico

A continuación calcularemos el precio sombra de una restricción del siguiente modelo de Programación Lineal:

La solución óptima de este modelo es X=100 e Y=350 con valor óptimo V(P)=3.100 según su resolución gráfica con Geogebra o su resolución con Solver de Excel. El siguiente diagrama muestra la solución óptima obtenida gráficamente en el vértice C, que corresponde a la intersección de la restricción 1 (R1: color rojo) y la restricción 3 (R3: color gris), siendo ésta una solución básica factible óptima.

Supongamos que deseamos saber cuánto cambiará el valor óptimo (respecto a su valor actual) si aumenta en una unidad el lado derecho de la restricción 1 pero sin resolver nuevamente el problema. El precio sombra nos permite dar respuesta a dicha interrogante y permite anticipar el nuevo valor óptimo ante una variación marginal del lado derecho de una restricción.

Un variación marginal de un lado derecho implica que la nueva solución óptima se seguirá encontrando con las actuales restricciones activas, es decir, aquellas que se cumplen en igualdad en el óptimo (esto es se conserva la base óptima).

En el caso de la restricción 1 si aumentamos su lado derecho, ésta se desplazará en forma paralela hacia arriba. Si buscamos garantizar que la nueva solución óptima aún se encontrará con R1 y R3 activas llegaremos al vértice donde actualmente se interceptan la R2 y R3 que corresponde a la coordenada X=166,67 e Y=350 (ésta será la máxima variación).

En forma análoga si disminuimos el lado derecho de la restricción 1 y buscamos mantener R1 y R3 activas en el nuevo óptimo, el último punto donde se garantiza esto es el vértice B cuyas coordenadas son X=0 e Y=350 (ésta será la menor variación). Con esta información calculamos el precio sombra de la restricción 1:

Este precio sombra es válido si el lado derecho de la restricción 1 (actualmente b1=1.600) varía entre [1.400,1.733,33]. Por ejemplo, si el lado derecho de R1 aumenta de 1.600 a 1.700 el nuevo valor óptimo será V(P)=3.100+100*1,5=3.250. Análogamente si el lado derecho de R1 disminuye de 1.600 a 1.550 el nuevo valor óptimo será V(P)=3.100-50*1,5=3.025. (Se recomienda corroborar estos resultados gráficamente con TORA o IORTutorial). Notar que si la variación del lado derecho de la restricción 1 está por fuera del intervalo [1.400,1.733,33], no se puede utilizar el precio sombra para predecir cuál será el nuevo valor óptimo.

En un próximo análisis complementaremos el cálculo del precio sombra de las restricciones 2 y 3 en conjunto con otros Análisis de Sensibilidad en la resolución de modelos de programación lineal. Hasta entonces!

Preguntas Frecuentes (Procesos): Capacidad, Tiempo de Flujo, Tiempo de Ciclo

Para desarrollar un análisis cuantitativo de procesos productivos (proceso de transformación de insumos en productos o servicios) generalmente se hace referencia a indicadores de gestión que permiten evaluar el desempeño y eficiencia de dicho proceso en el tiempo. Algunos de los indicadores más utilizados son capacidad, tiempo de flujo y tiempo de ciclo. A continuación los definimos brevemente para luego aplicarlos a un ejemplo tipo:

Capacidad de un Proceso: corresponde a la tasa máxima de producción, es decir, cuántas unidades en un intervalo de tiempo un proceso (sistema) puede producir.
Tiempo de Flujo: es el tiempo de producción, es decir, es el tiempo mínimo total que una unidad se demora en pasar por el sistema.
Tiempo de Ciclo: es el tiempo promedio entre la producción de dos unidades consecutivas.

A continuación presentaremos un proceso de producción sencillo de fabricación de muebles.

La Capacidad del Proceso es de 10 [u/hora]
El Tiempo de Flujo (para la primera unidad) es de 19 [min] (5+8+6)
El Tiempo de Ciclo del proceso es de 6 [min] (si se producen 10[u/hora] en promedio se produce una cada 6[min])

Las siguientes preguntas frecuentes nos permitirán entender mejor los conceptos relacionados con los procesos productivos:

1. ¿Si se dobla la capacidad de la actividad cuello de botella entonces se doblará la capacidad del proceso?.

Falso. Esto no es cierto en todos los casos. En nuestro ejemplo la actividad cuello de botella es Pintar y su capacidad es de 10[u/hora] (recordar que la capacidad conjunto de las etapas Ensamblar es de 13,5[u/hora]). Si doblamos la capacidad de Pintar su nueva capacidad será ahora 20[u/hora] y ahora el cuello de botella es Pulir. La nueva capacidad del proceso es de 12[u/hora] lo que no es el doble de la capacidad original.

2. ¿En una hora de trabajo se producirán exactamente las unidades que indica la capacidad del proceso?.

Falso. De otra forma en la primera hora de trabajo no se alcanzan a producir las 10[u/hora] que indica la capacidad del proceso. ¿Por qué?. La razón es que la(s) primera(s) unidad(es) se demoran más que las unidades cuando el proceso se encuentra estabilizado. Por ejemplo, la primera unidad sale del sistema a los 19[min] (tiempo de flujo), la segunda unidad sale a los 26[min] (7 minutos después de la primera), la tercera, cuarta, quinta, etc, unidades salen cada 6[min] (tiempo de ciclo) lo que permite anticipar que las unidades que sigan saldrán en promedio cada 6[min]. La Carta Gantt a continuación permite visualizar el proceso en su primera hora donde queda de manifiesto que no se alcanzan a procesar en forma completa las 10 unidades.

3. ¿Cómo determinar entonces cuántas unidades completas se alcanzan a procesar en la primera hora de trabajo?.

Para ello utilizamos la siguiente fórmula:

T(N)=TF+(1/Cap)*(N-1)

En nuestro ejemplo: 60[min]=19[min]+6[min/u]*(N-1) ==> N=7,833[u] ~ 7[u]

Es decir, se alcanzan a producir en forma completa 7 unidades en la primera hora. Notar que esto no contradice la capacidad del proceso. Si tomamos un horizonte de tiempo más amplio (2 horas, 3 horas, etc) la cantidad de unidades que se puedan procesar en promedio en una hora convergerá a la capacidad del proceso que es de 10[u/hora]. El motivo de lo anterior es que cada vez el efecto de las primeras unidades (hasta la estabilización del proceso) es menor.