tutoriales Archivos - Página 8 de 11 - Gestión de Operaciones

Cómo resolver un modelo de Programación Lineal con What’sBest!

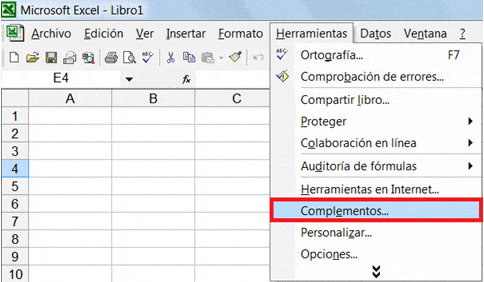
En el siguiente tutorial mostraremos Cómo resolver un modelo de Programación Lineal con What’sBest!. Para ello por supuesto se requiere previamente descargar e instalar What’sBest! como complemento de Excel tal cual lo explicamos paso a paso en un artículo previo.

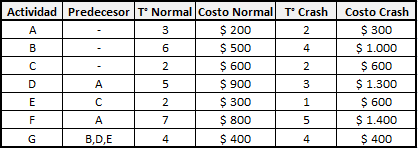
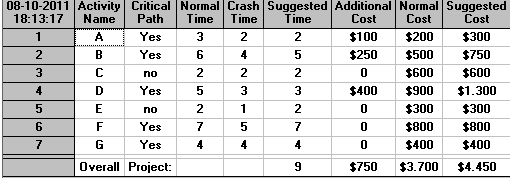
Para mostrar cómo utilizar este programa utilizaremos el Problema de Transporte que consiste en determinar una política de distribución que minimice los costos de la logística, al mismo tiempo que satisface la demanda de los clientes y respeta la capacidad de los oferentes.

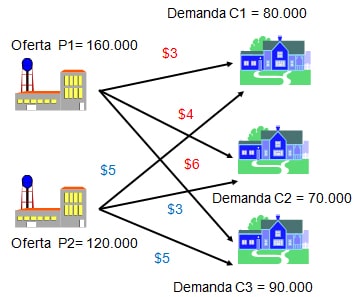
La información se resume en el siguiente diagrama para un caso particular de 2 plantas y 3 clientes, donde los números sobre las flechas representan los respectivos costos unitarios de transporte entre una planta y un cliente.

Los pasos para implementar este problema de programación lineal en What’sBest! son:

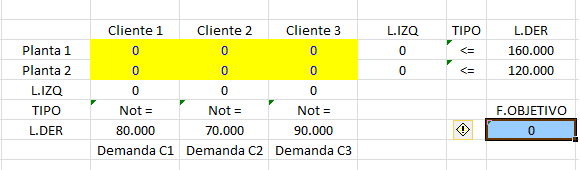
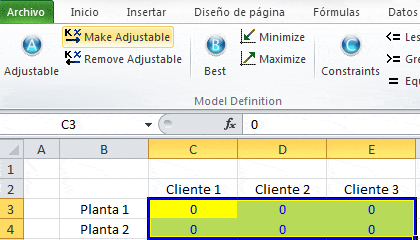
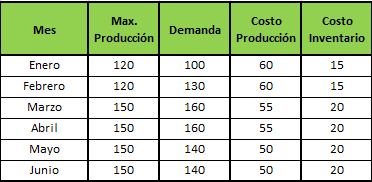
Paso A: Definir las Variables de Decisión: Para ello debes previamente definir en un planilla Excel las celdas que utilizarás como variables. En el ejemplo la Xij: Unidades transportadas desde la planta i al cliente j. Con i=1,2 y j=1,2,3 se tienen 6 variables de decisión.

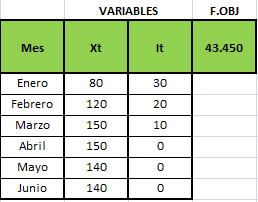
Importante: Completa las celdas que serán variables de decisión con cero como se muestra en la imagen anterior. Luego selecciona el rango de celdas que corresponde a las variables del modelo y presiona «Make Adjustable».

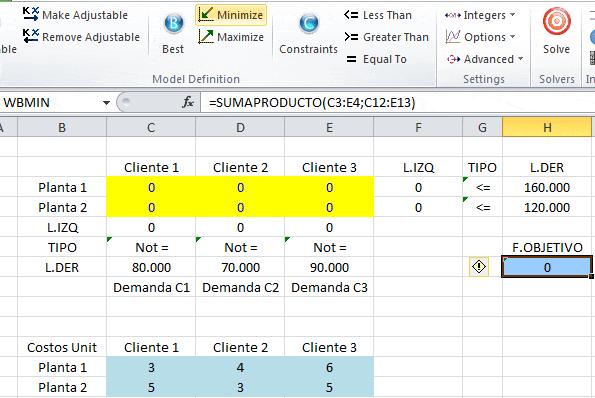
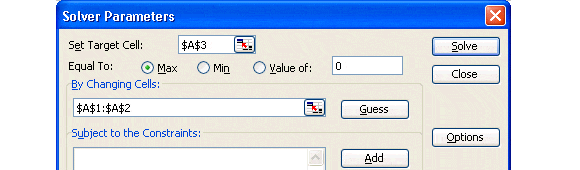
Paso B: Definir la Función Objetivo: Como el nombre lo indica, ésta celda corresponde al objetivo del problema de optimización que en este caso es minimizar los costos totales de transporte. La celda contiene una fórmula SUMAPRODUCTO(C3:E4;C12:E13) previamente ingresa que pondera los costos unitarios de transporte para las distintas combinaciones (datos o parámetros) y las variable de decisión previamente definidas. Finalmente nos posicionamos sobre la celda de la función objetivo y seleccionamos en este caso «Minimize».

Paso C: Definir las Restricciones: Se incorporan las restricciones del modelo de optimización, es decir, las condiciones que deben cumplir las variables de decisión al momento de la resolución. Para ello se selecciona en el menú la opción «Constraints».

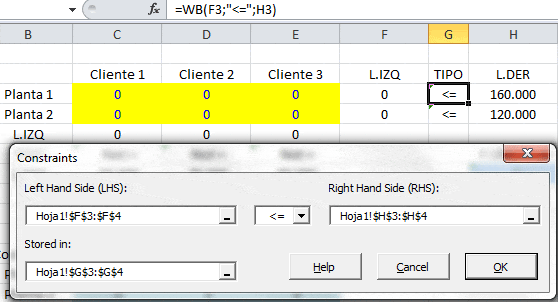
En la imagen a continuación se muestra cómo se incorporó la restricción que garantiza que la cantidad de unidades enviadas por cada planta (L.IZQ) no supere (<=) la capacidad de la misma (L.DER). Como se puede apreciar se incorporan las restricciones de capacidad de la planta 1 y 2 en forma simultanea.

Finalmente para proceder a la resolución del modelo seleccionamos la opción «Solve» del menú:

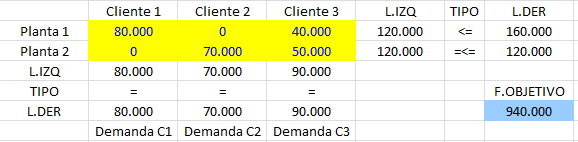
Luego de lo cual se obtienen los siguientes resultados:

Solución Básica Factible Óptima: X11=80.000; X12=40.000; X13=0; X21=0; X22=30.000; X23=90.000. El Valor Óptimo (mínimo costo) es de $940.000. Para descargar el archivo Excel con la resolución del modelo de transporte con What’sBest! sigue los pasos a continuación:

[sociallocker]Descarga Aquí: https://www.gestiondeoperaciones.net/wp-content/uploads/2013/02/PTWB.xlsx[/sociallocker]

Problema de Construcción de Viviendas resuelto Gráficamente

El siguiente problema fue enviado por uno de nuestros usuarios de la ciudad de Bogotá, Colombia:

En la ciudad de Armenia se va a demoler un barrio de 10 acres y la alcaldía debe decidir sobre el nuevo plan de desarrollo. Se van a considerar dos proyectos habitacionales: viviendas a bajo costo y viviendas a medio costo. Se pueden construir 20 y 15 unidades de cada vivienda por acre, respectivamente. Los costos por unidad de las viviendas a bajo y medio costo son $13.000 y $18.000, respectivamente. Los límites inferior y superior establecidos por la alcaldía sobre el número de viviendas de bajo costo son 60 y 100 respectivamente. De igual manera, el número de viviendas de costo medio debe estar entre 30 y 70. Se estima que el mercado potencial combinado máximo para las viviendas es de 150 (que es menor que la suma de los límites de los mercados individuales debido al traslapo entre los dos mercados). Se desea que la hipoteca total comprometida al nuevo plan de desarrollo no exceda los $2 millones. Finalmente, el asesor de la obra sugirió que el número de viviendas de bajo costo sea por lo menos de 50 unidades mayor que la mitad del número de viviendas de costo medio.

Formule como un Programa Lineal el problema del nuevo plan de desarrollo a costo mínimo y resuelvalo gráficamente.

A continuación detallamos la resolución de este problema de Programación Lineal utilizando el Método Gráfico:

1. Variables de Decisión:

X1: Viviendas de bajo costo a construir
X2: Viviendas de costo medio a construir

2. Función Objetivo: Minimizar 13.000X1 + 18.000X2

3. Restricciones:

Disponibilidad de acres: (X1/20) + (X2/15) <= 10
Límites de viviendas de bajo costo: 60 <= X1 <= 100
Límites de viviendas de costo medio: 30 <= X2 <= 70
Límite mercado combinado: X1 + X2 <= 150
Límite hipoteca total: 13.000X1 + 18.000X2 <= 2.000.0000
Sugerencia asesor de obra: X1 >= 50 + (X2/2)
No Negatividad: X1>=0 X2>=0

La resolución gráfica del modelo de programación lineal anterior se muestra a continuación utilizando el software Geogebra:

Solución Básica Factible Óptima: X1=65 y X2=30
Valor Óptimo: V(P)=$1.385.000

Problema de Producción e Inventario resuelto con Solver de Excel

La Programación Lineal nos permite abordar distintos problemas de naturaleza real algunos de los cuales ya hemos tratado en artículos anteriores como el Problema de Transporte, el Problema de Mezcla de Productos y el Problema de la Dieta.

En el siguiente artículo analizaremos otra aplicación clásica conocida como el Problema de Producción e Inventario cuyas extensiones y variantes se pueden consultar adicionalmente en la categoría del Plan Maestro de la Producción.

El Problema de Producción e Inventario consiste básicamente en determinar una política de producción en el tiempo que permita satisfacer ciertos requerimientos de demanda, respetando las limitantes de producción y a un costo mínimo.

Este tipo de modelos se puede extender para varios productos, sin embargo, en esta oportunidad consideraremos un solo producto para su ilustración.

En este contexto, consideremos los siguientes antecedentes de producción que se presentan a continuación:

Luego, definimos el siguiente modelo de optimización lineal:

Supuesto: se dispone de un inventario inicial de 50 unidades, es decir, I0=50.

1. Variables de Decisión:

Xt: Unidades a producir en el mes t (t=1,..,6 con t=1 => Enero; t=6 => Junio)
It: Unidades a almacenar en inventario al final del mes t (t=1,..,6 con t=1 => Enero; t=6 => Junio)

2. Función Objetivo: Minimizar los costos de producción (destacados con color azul) y costos de inventario (destacados con color rojo) durante el período de planificación definido por:

60X1 + 60X2 + 55X3 + 55X4 + 50X5 + 50X6 + 15I1 + 15I2 + 20I3 + 20I4 + 20I5 + 20I6

De forma compacta (parametrica) se puede representar la función objetivo como:

$Minimizar\sum_{t=1}^{6}[C_{t}\cdot X_{t}+H_{t}\cdot I_{t}]$

Donde $C_{t}$ es el costo unitario de producción en el mes t (por ejemplo $C_{1}=60$ ) y $H_{t}$ es el costo unitario de almacenar unidades en inventario durante el mes t (por ejemplo $H_{1}=15$ )

3. Restricciones:

a) Satisfacer los requerimientos de demanda (conocida como restricción de Balance de Inventario).

Por ejemplo, el inventario disponible al final del mes de Enero será el resultado de la producción del mismo mes, más el inventario inicial (que se asume un dato, en este caso 50 unidades) menos la demanda satisfecha durante el mes de Enero.

X1 + 50 – I1 = 100 (Enero)
X2 + I1 – I2 = 130 (Febrero)
X3 + I2 – I3 = 160 (Marzo)
X4 + I3 – I4 = 160 (Abril)
X5 + I4 – I5 = 140 (Mayo)
X6 + I5 – I6 = 140 (Junio)

Notar que la restricción se Balance de Inventario impuesta para un producto se puede generalizar como: $X_{t}+I_{t-1}-I_{t}=d_{t}$ , donde $d_{t}$ representa la demanda estimada (parámetro) para el mes t.

b) Respetar la capacidad máxima de producción mensual (oferta).

Se establece que la oferta o producción máxima mensual no puede superar la capacidad de producción.

X1<=120 X2<=120 X3<=150 X4<=150 X5<=150 X6<=150

O simplemente $X_{t}\leq O_{t}$ donde $O_{t}$ es la capacidad de producción máxima del mes t (parámetro).

c) Condiciones de no negatividad.

De forma natural y dada nuestra definición cada variable de decisión debe ser no negativa.

Xt >= 0 It >= 0 Para todo t

El siguiente tutorial muestra cómo implementar este Modelo de Producción e Inventario correspondiente a la Programación Lineal en Solver de Excel:

La solución óptima se muestra a continuación con un valor óptimo de $43.450. Se puede apreciar que se producen en total 780 unidades entre Enero y Junio las cuales junto al inventario inicial de 50 unidades permiten satisfacer los requerimientos de demanda mensualmente.

¿Quieres tener el archivo Excel con la resolución en Solver de este problema?.

[sociallocker]

MUCHAS GRACIAS!. DESCARGA AQUÍ EL ARCHIVO

[/sociallocker]

Instalación del Complemento Solver en Excel 2003

El complemento de Solver de Excel es una poderosa herramienta que permite resolver modelos de optimización utilizando una planilla de cálculo (Excel). En artículos anteriores hemos mostrado Cómo resolver Modelos de Programación Lineal utilizando Solver y algunas aplicaciones clásicas como el Problema de Transporte y Problema de la Dieta.

Las características de Solver han evolucionado en las distintas versiones de Office y en esta oportunidad mostraremos cómo activar este complemento en la versión del año 2003 y 2007. Para ello se deben seguir los siguientes pasos:

Paso 1: Abrir el programa Excel y en el menú de Herramientas seleccionar Complementos.

Paso 2: Seleccionar la opción Solver y luego Aceptar.

Paso 3: Puede ser necesario aprobar la ejecución del complemento como muestra la imagen a continuación. En este caso se debe seleccionar Sí

Paso 4: Una vez completada la activación de Solver el complemento estará disponible en el menú de Herramientas de Excel.

Una alternativa a Solver es el complemento de Excel OpenSolver el cual se puede descargar gratuitamente desde www.opensolver.org. En el artículo Cómo resolver un modelo de Programación Lineal con OpenSolver mostramos su utilización en un problema sencillo. Adicionalmente What’sBest! resulta ser otra excelente alternativa para Solver y desarrollado para Excel. En el siguiente tutorial detallamos cómo descargar e instalar What’sBest!.

Cómo reducir la duración de un Proyecto (Crashing) con WINQSB

Un aspecto relevante en todo Proyecto es lograr estimar el tiempo necesario para completar las distintas actividades que lo conforman. En artículos anteriores hemos analizado el Método de Ruta Crítica (CPM) y la Metodología PERT, asumiendo tiempos de actividades deterministas (fijos) y aleatorios (probabilísticos), respectivamente.

En esta oportunidad consideraremos un Proyecto que consta de 7 actividades y que en condiciones de tiempo normal tiene por Ruta Crítica a las actividades A-D-G con una duración total de 12 semanas:

La tabla anterior incluye adicionalmente información sobre el costo normal de desarrollar las actividades en condiciones de tiempo normal y el tiempo crash que consiste el menor tiempo en el que se podría llevar a cabo la actividad en caso que se «apure».

En muchos proyectos existen actividades que podrían demorar menos si se invirtiera más recursos en ellas (costo crash), sin embargo, hay actividades que no son factibles de acortar (por ejemplo, podría ser el tiempo requerido para obtener un permiso por parte de una oficina del gobierno central, asunto que esta fuera del alcance del gerente del proyecto).

Por ejemplo, si quisiéramos reducir el tiempo de la actividad A de 3 a 2 semanas el costo incremental es de $100. Análogamente el costo de reducir el tiempo de la actividad B en 1 semana sería de $250 (se asume proporcionalidad).

El costo actual del proyecto es de $3.700 (suma de los valores de la columna «Costo Normal») para un tiempo estimado de 12 semanas (A-D-G Ruta Crítica).

Si queremos que el proyecto se demore menos de 12 semanas debemos estar dispuestos a asumir un costo monetario mayor. En este contexto el Análisis de Crashing (reducir la duración de un proyecto a un costo eficiente) resulta vital.

El siguiente tutorial muestra cómo reducir la duración de un proyecto utilizando el software WINQSB:

El menor tiempo en el cual se puede desarrollar el proyecto es 9 semanas con un costo total de $4.450. Para ello se reduce el tiempo de las actividades A y B en 1 semana y D en 2 semanas. Las Rutas Críticas ahora son: A-F ; A-D-G; B-G todas con 9 semanas según se muestra en el siguiente informe de WINQSB:

Es importante destacar que NO se puede seguir reduciendo la duración del proyecto aún cuando algunas actividades aún son factibles de apurar. Esto se justifica en general porque al menos una Ruta Crítica no se puede reducir y en dicho caso no tiene sentido destinar más recursos si esto no se verá reflejado en la duración total del proyecto. Por ejemplo, aún podemos reducir la duración de B de 5 a 4 semanas, sin embargo, la duración de la ruta A-D-G no se puede seguir reduciendo.

Importante: Recomendamos revisar el artículo Formulación y Resolución de un Modelo de Programación Lineal para reducir la duración de un Proyecto (Crashing) que detalla cómo a través de un modelo de optimización encontrar aquellas actividades que deben reducir su duración de modo de desarrollar el proyecto en el menor costo posible (dado un tiempo objetivo). En este contexto un artículo complementario es Cómo determinar la Duración Óptima de un Proyecto a través del Análisis de Crashing.